Publications of Dr. Martin Rothenberg:

Speech Communication Seminar Stockholm. Aug. 1-3. 1974

Abstract
A "black box" model of the voice source has been built. This model has as inputs three physiologically derived variables and an output wave form similar to the actual glottal volume velocity wave. The voice source has been used with the OVE III serial formant synthesizer and this paper reports on some preliminary synthesis experiments using a new rule synthesis system.

Introduction
Until recently, speech synthesizers have used a simple representation of the voice source, usually a pulse source of slowly varying frequency and amplitude, augmented by a noise source for use during glottal fricatives. It is generally recognized that the actual voice source differs from this simple model in that the quasi-periodic glottal pulses are constantly changing in spectral distribution, and have noise components and other irregularities not modeled by a pulse source of slowly varying frequency and amplitude. Also, in normal speech these acoustical parameters are not varied independently, but are controlled by the more fundamental physiological mechanisms for pitch control, glottal abduction and adduction, laryngeal constriction, and subglottal pressure regulation (Ladefoged, 1973. Lindqvist, 1972). A mechanism for raising and lowering the whole larynx is also important in languages employing ejectives or implosives.

The approaches taken by Fujimura (1968) and by Ishizaka and Flanagan (1972) illustrate two rather different ways to model the glottal source more closely. We might call these the acoustical and the physiological approaches. Fujimura used the usual quasi-periodic pulse source during voicing, but in a way that made it more similar acoustically to an actual source, in this case by irregularly alternating noise and periodic excitation in some of the higher frequency bands. On the other hand, Ishizaka and Flanagan attempted to use a computer-based model of the laryngeal source to produce a replica of the glottal wave.

The acoustical approach is often simplest to implement, when the correct acoustic parameters, and the rules for their use, have been identified. The physiological approach, however, introduces in a natural way parameters whose effects are not yet known, for example the effects of context on voice quality, that is, the effects of the simultaneous supraglottal articulation and the effects of the preceding and following phonetic segments. The physiological approach presupposes a reasonably accurate model of the glottal source.

We report here on an approach intermediate to the acoustical and physiological methods. We have attempted to develop a behavioral or "black box" model of the glottal source. This model would have as inputs physiologically derived variables, and as an output a waveform similar to the actual glottal volume velocity wave. However, the internal operation of the model would not necessarily have any physiological relevance. We have found that a behavioral model is especially well-suited to the primary data we have used in its development, namely glottal air flow waveforms obtained by inverse-filtering the volume velocity waveform at the mouth (Rothenberg, 1973).

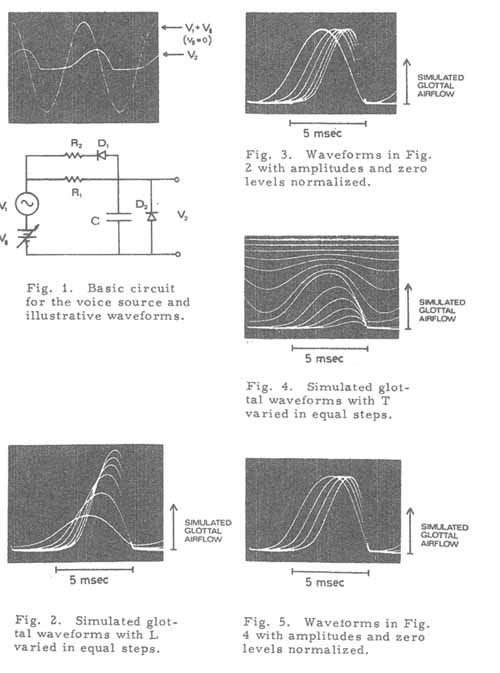
Voice source circuitry
Our model of the voice sqilrce makes use of a simple electrical network shown in Figure 1, that for appropriate values of its parameters produces an output waveform V₂ similar to a typical glottal waveform during normal voicing. Its operation can be explained as follows. When the diodes D₁ and D₂ are not conducting (when V₂ > [V₁ + V_B] and V₂ > 0, as in the rising segment of V₂, the low pass filter formed by R₁ and C tends to produce a sinusoidal output that is smaller than the input, and delayed by up to 1/4 cycle. depending on the frequency. However, when V₂ gets larger than [V₁, + V_B] (the time at which the two curves cross in the oscilloscope photo) the diode D₁ conducts, and V₂ falls more rapidly than it rose. The steep falling phase of V₂ is interrupted when V₂ becomes negative and D₂ conducts to hold V₂ just be1ow zero volts. V₂ stays zero until [V₁ + V_B] becomes positive once more, and then V₂ rises slowly, as controlled by the time constant R₁C. In the actual circuit used, the branch R₂D₁ was replaced by a more complex resistor diode network to improve the falling segment of the waveform. The waveform V₂ shown was generated by the more complex network.

Over a limited range, the circuit shown in Figure 1 can be easily controlled to produce changes in the waveform roughly similar to changes produced by three important physiological parameters of the voice source. An increase in the frequency of V₁, in addition to increasing the frequency of V₂, also reduced the amplitude of V₂ somewhat, thus simulating the effect of increasing longitudinal vocal cord tension. Small changes in the amplitude of V₁ produce changes in the waveform roughly similar to what one may expect from changes in P_sg. By varying the dc voltage V_B one could get either smaller, narrower pulses (V_B negative) or larger, broader pulses (V_B positive). This action appears to simulate well the effect of changing the degree of adduction or abduction on the vocal folds (Rothenberg. 1973).

The basic circuit of Figure 1 was incorporated into a complex electrical network designed to represent our "best guess" as to how a set of three control voltages representing neurological command parameters F (frequency), L (loudness), and T (tightness) are related to the glottal air flow waveform, for an unconstricted supraglottal vocal tract. Filtered gaussian noise was added to the waveform in a manner meant to simulate the occurrence of noise in the actual glottal wave (Rothenberg, in preparation). Since the basic waveform shown in Figure 1 still did not have the steep termination of the glottal closing phase characteristic of natural waveforms, it sounded somewhat deficient in high frequencies when used for synthesis. The termination was made steeper by adding a component [1.8x10^-4dV₂/dt], with the constant chosen by informal listening tests as the minimum sufficient to produce adequate high frequency energy. Some of the effects of the acoustic interaction between the glottis and the subglottal and supraglottal systems are included in the model, since the waveforms obtained by inverse-filtering that have been used as comparison guides do contain these effects. However, other effects are not present, such as oscillations in the rising phase at the frequency of the first formant (representing the change in first formant damping), and differences correlated with the vowel value. The operation of the complete model is illustrated by the sample waveforms shown below.

Varying frequency
In the voice source model, frequency is varied linearly by the F parameter. In addition, raising the tightness parameter T above a preset level, illustrated below, results in a sharp decrease of fundamental frequency, followed by a small range of T in which irregular, low frequency pulses occur. Higher values of T extinguish glottal oscillations entirely.

There is provision in the model for varying frequency slightly in proportion to L, to simulate the dependence on subglottal pressure. However, this provision was not used in the synthesis experiments so far.

The small random or systematic variations of the periodicity of the voice source sometimes found in the human voice were not added. However some degree of aperiodicity that could be termed '"frequency jitter" is introduced by the additive random noise.

Varying loudness
There is as yet no conclusive evidence as to the way the waveform varies with changes in the various amplitude related voice parameters such as subglottal pressure, perceived loudness, subjective voice effort, or the various types of stress found in natural speech. However, the waveforms shown by Lindqvist (1970) and Rothenberg (1973) indicate that the peak-to-peak amplitude of the glottal air flow pulses would increase only slightly with increased loudness (less than the percentage increase in subglottal pressure) with the pulses getting narrower and having a steeper closing phase. The intensity change is thus mainly caused by a change in the voice source spectrum and not by an increasing amplitude of the source. The observed change in the source waveform can be explained by an increase in the pressure drop across the glottis, but we cannot exclude the possibility that some rearrangement of the laryngeal muscles is made, even if this has not been experimentally shown in a conclusive way (Hirano, Ohala. and Vennard, 1969). Increasing subglottal pressure also causes the fundamental frequency to raise which by itself has the effect of increasing the voice intensity (Fant and Liljencrants, 1962).

Figure 2 shows the variation in the waveform of the artificial voice source, as the loudness parameter is varied in six equally spaced steps to the maximum possible. The F parameter was set for a glottal period of about 8 msec, and the T parameter for a normal or average adduction of the vocal folds. The dependence of fundamental frequency on L was removed to facilitate comparison of the waveforms. The steps in L shown might be considered roughly equivalent to values of subglottal pressure of 2.5, 5, 7.5, 10, 12.5, and 15 cm H₂O, with 8 cm H₂O being a typical average value in quiet conversation. These waveforms show, at least approximately, the desired variation in waveform and amplitude.

To further facilitate the comparison of the wave shapes in Figure 2, these same waveforms are shown in Figure 3 normalized in both zero level and peak amplitude. It is easy to see that an increase in L increases the high frequency content of the waveform, with an increase in the ratio of the energy in the region of the second and third formants to the average air flow.

Varying "Tightness"
The T control parameter corresponds approximately to the physiological dimensions "glottal abduction" and "laryngeal closure" as described by Lindqvist (1972). Increasing T from zero simulates glottal adduction articulation until a level is reached where the glottis is in voicing position. If T is further increased, "laryngeal closure" is simulated. Accordingly, the T parameter is similar to the "glottal stricture" dimension used by Ladefoged (1973).

Figure 4 shows the variation of the waveform of the voice source model for 13 equally spaced steps of the T parameter, with the L parameter constant at what would be considered an average conversational level (1/2 of its maximum value) and the period kept constant at 8 msec. In our attempts at speech synthesis. the fourth trace from the bottom was considered to have an average or normal "tightness". As the T parameter was increased from its normal value, the pulses became smaller and somewhat narrower. At the level indicated by the second trace from the bottom, the period would begin to lengthen if it had not been kept constant for the picutre. At the level of T corresponding to the lowermost trace, the period would be very long and possibly unstable. Any further increase in T would terminate the oscillations.

Decreasing T below its normal value makes the simulated glottal pulse broader and more smoothly varying, as would occur if the vocal folds came together for a shorter period, with a lower velocity at the instants of closure and separation. By the sixth trace from the bottom, the flat part of the wave is offset from zero, indicating that the vocal folds would not be approximating over their entire length. (In such cases the incomplete closure usually occurs posteriorly between the arytenoid cartilages.) There would be little energy in this waveform above the fourth or fifth harmonic. A further decrease in T (seventh trace from the bottom) results in a waveform that is almost sinusoidal, as might occur if the vocal folds oscillated without coming in contact. As T decreases further, the oscillations become smaller, with some flattening on top. as compared to a sinusoid, and noise can be more clearly seen on the waveform. Noise can also be seen to increase for the most tight waveforms.

To facilitate the comparison of the waveforms. the third through sixth waveforms from the bottom in Figure 4 are shown again in Figure 5, but normalized in zero level and amplitude. Changes in the normalized waveshape can be seen to be similar to those which occur when the L parameter is varied. This is to be expected, since we have hypothesized that a pressure-induced increase in the loudness includes increase in the adduction of the vocal folds.

Use of the voice source in synthesized speech
To explore the dynamic capabilities of the voice source it has been linked to the new rule synthesis system at the Department of Speech Communication, KTH (Carlson and Granström, 1974, this Seminar). The three parameters of the source were controlled via separate digital to analog converters and the output of the source was connected to our OVE III serial formant synthesizer. Since the internal pulse amplitude, pulse frequency, and glottal noise (aspiration) controls of the synthesizer were thus made unnecessary, the number of control parameters remained constant.

In our old synthesis system, the main interest has been focused on the description of supraglottal articulation, since glottal articulation, at least from a phonemic standpoint, is relatively unimportant in the languages we mostly have worked with. i.e. Swedish and English. However, the expectations with the new source are not so much for better segmental intelligibility as for increased segmental and supra-segmental naturalness, primarily due to more natural transitions between different states of the glottis and the incorporation of prosodically controlled source changes. The nature of the control parameters should also fit a more elegant and less ad hoc formulation of some synthesis rules.

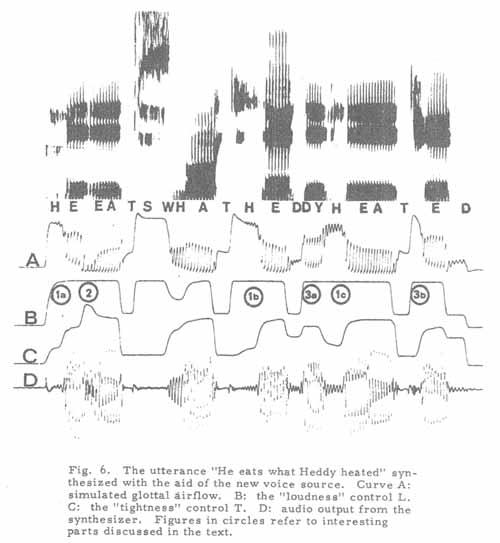
Some examples where we feel that this is the case will be given below. The synthesis is based on smoothed step commands (Liljencrants, 1971) so the control problem is reduced to assigning the appropriate extent and timing of the steps and the characteristics of the step smoothing. The rules under discussions will be illustrated by the synthesized sentence "He eats what Heddy heated" that can be seen in Figure 6.

Signaling of constituent boundaries
When two vowels close in quality are contiguous phonemically but separated by a constituent boundary, the boundary is marked by a simulated glottal stop gesture, as produced by a brief positive tightness command (point 2 in Figure 6). As can be seen, the pulse amplitude and the frequency are lowered very much as in natural speech. This kind of gesture can also be used for disambiguiting phrases like "an ice man" and "a nice man" (Lehiste, 1959).

Allophonic variations in [ h ]
[ h ] tends to be voiceless in post-pausal and post-unvoiced positions but voiced in voiced contexts. This is clearly a matter of coarticulation that can easily be described as such by always associating an [ h ] with a moderately negative going step in the tightness parameter. The effect of this could be seen in Figure 6 at points 1a, 1b, 1c.

Non-nasal consonants with supraglottal constriction
For these kinds of sounds, several aspects of the glottal source have to be taken into account in addition to the two obvious modes, voiced and unvoiced. If the constriction is complete, as in stops, or only slightly open, the supraglottal pressure increase gives a reduction of transglottal pressure. This corresponds to a lowering of the L parameter, however. the change has to be made differently depending on whether the constriction is complete or not.

During an unvoiced stop occlusion the voice source output should be zero. This is automatically obtained by setting the T parameter to a low value appropriate for voiceless sounds while simultaneously lowering L. These changes are relatively rapid, since they are due to only a small part of the total movement of the tongue or the lips, and could not be expected to follow time constants typical for glottal adjustment. Hence the source parameter time constants associated with these articulatory changes have been made to be approximately twice as fast as the parameter variations related to glottal and subglottal dynamics.

Since the synthesizer does not model radiation from the walls, the voiced murmur of a voiced stop has been introduced functionally by setting the L and T parameters to values that result in a fairly steep spectral slope of the voice source.

When the release occurs in a stop, the L parameter is raised. This results in a simulated aspiration if T is kept constant, or normal voicing if T is raised simultaneously. The aspiration is accordingly introduced in the synthesis as the normal articulatory delay in pulling the vocal folds together. These effects are illustrated in Figure 6, points 3a and 3b.

In the synthesis of the release of a stop, a short burst of energy is introduced to simulate the energy generated at the articulators by the explosion. The noise source during aspiration following the explosion does not have to be entirely at the glottis. It could be higher up in the vocal tract in the region of epiglottis or even at the main constriction, resulting in something like a homorganic fricative in the context of front vowels, and sometimes causing a phonological shift from stop to affricate (English) or fricative (Swedish). This aspiration variation has not yet been taken into account in our model, however.

Unvoiced fricatives, as the [s] in Figure 6, are produced with the energy generated at the articulatory constriction added separately, but with a glottal control similar to that for an [h]. In this way, glottal coarticulation effects occur in a natural manner.

Voiced fricatives and semivowels, as the [w] in Figure 6, are produced by using values for L and T that differ from normal voicing values in the proportions used for a voiced stop, but differ from normal voicing only about half as much as for the stop. The time constant for these changes is slower than for a stop.

Lexical stress and Linguistic marking
The relation between subglottal pressure and prosody has been shown to be quite close (Ladefoged. 1968). In our synthesis rules supra-segmental factors are manifested by relatively slow variations in L and F₀. The lexical stress marking, however, is not so clear and can be simulated perceptually by either a T or an L change. dependent on whether the innervation of the larynx or the subglottal system is believed to be the most important. In the example of Figure 6, lexical stress was signalled in part by a different value for T during the vowel.

Summary
Our model of the voice source assumes that the three control parameters F, L, and T are adequate for the synthesis of the target languages. Swedish and English, and are related to the acoustical parameters of frequency. amplitude. spectral distribution and aperiodicity in ways similar to those inherent in the model. These assumptions are supported by our success so far in synthesizing many types of natural sounding glottal transitions using relatively simple rules. However, we feel that much more independent verification is needed for the relationships between the physiological parameters and their acoustic consequences. For example. more information is needed on the effect of the transglottal pressure on the glottal waveform.

It is also not clear whether the control parameter L should include changes of laryngeal adjustment, as now, or should reflect only the effect of changes in transglottal pressure.

References
Carlson, R. and Granström, B.: "A phonetically oriented programming language for rule description of speech", Speech Communication Seminar, Stockholm 1974.

Fant. G. and Liljencrants, J.: "How to define formant level. A study of the mathematical model of voiced sounds", STL-QPSR 2/1962, pp. 1-9.

Fujimura, O.: "An approximation to voice aperiodicity", IEEE Trans, on Audio and Electroacoustics, AU-16, March 1968, pp. 68-72.

Hirano, M., Ohala, J., and Vennard, W.: "The function of laryngeal muscles in regulating fundamental frequency and intensity of phonation", JSHR. 12 (1969). pp. 616-628.

Ishizaka, K. and Flanagan, J.: "Synthesis of voiced sounds from a two-mass model of the vocal cords", Bell System Technical Journal. 51 (1972), pp. 1233-1268.

Ladefoged, P.: "Linguistic aspects of respiratory phenomena", Ann. of the New York Academy of Sciences, 155, November 20, 1968.

Ladefoged, P.: "The features of the larynx", J. of Phonetics, 1 (1973), pp. 73-83.

Lehiste, I.: "An acoustic-phonetic study of internal open juncture", Report no. 2, Speech Research Lab., University of Michigan, Aug. 1959.

Liljencrants, J.: "Computer vocal response system using smoothed step commands", paper 24 E 5 presented at the Seventh International Congress on Acoustics, Budapest 1971.

Lindqvist, J.: "The voice source studied by means of inverse filtering", STL-QPSR 1/1970, pp. 3-9.

Lindqvist, J.: "A descriptive model of laryngeal articulation in speech", STL-QPSR 2-3/1972, pp. 1-9.

Rothenberg, M.: "A new inverse-filtering technique for deriving the glottal air flow waveform during voicing", J.Acoust.Soc.Am. 53 (1973), pp. 1632-1645.

Rothenberg. M.: "Parameters of the voice source" (in preparation for the STL-QPSR).