Syracuse University, Syracuse, New York
(Received 9 August 1972; revised 27 November 1972)

Published in The Journal of the Acoustical Society of America
The Journal of the Acoustic Society of America, Vol. 53, #6, 1632 - 1645

ABSTRACT

A method is described for deriving the volume velocity waveform at the glottis during voiced speech by inverse-filtering the volume velocity waveform at the mouth. Unlike the previously used technique of inverse-filtering radiated acoustic pressure, this method provides a signal that is accurate down to zero frequency, not susceptible to low-frequency noise, and easily calibrated in amplitude by a constant air flow. The primary limitation is the need for a transducer that will measure volume velocity at the mouth with adequate fidelity. In this work, volume velocity was recorded from a specially designed circumferentially vented wire screen pneumotachograph mask which provided a time resolution of ½ msec, without serious speech distortion. Inverse-filtered volume velocity was recorded with two adult male subjects for voicing in the modal register. Typical results are shown which indicate the way in which the glottal waveform varied with changes of fundamental frequency, subglottal pressure, and a dimension of voice quality related to the degree of compression of the vocal folds. Also considered are the effects of glottal-supraglottal acoustic interaction, and the effect on the glottal waveform of air displaced by the movements of the vocal folds.

Subject Classification: 9.9, 9.3.

INTRODUCTION

In all proposed models for the production of speech, an important variable is the waveform of the air flow, or volume velocity, at the glottis. The glottal volume velocity waveform provides the link between movements of the vocal folds and the acoustical results of such movements, in that the glottis acts approximately as a source of volume velocity. That is, the impedance of the glottis is usually much higher than that of the vocal tract, and so glottal air flow is controlled mostly by glottal area and subglottal pressure, and not by vocal-tract acoustics. [1], [2]

A direct technique for obtaining the glottal volume velocity waveform during voiced speech is the “inverse-filtering” of the radiated acoustic waveform. [3-8] As practiced, inverse-filtering is usually limited to nonnasalized or slightly nasalized vowels. The acoustic signal is recorded using a pressure-sensitive microphone having an exceptionally good low-frequency response, and the recorded waveform is passed through an “inverse-filter” having a transfer characteristic that is the inverse of the transfer characteristic of the supraglottal vocal tract configuration at that moment. The transfer characteristic of the supraglottal vocal tract is defined with the input to the vocal tract considered to be the volume velocity at the glottis. For non-nasalized vowels, assuming a high-impedance volume velocity source at the glottis, the transfer function of the vocal tract below about 3000 Hz contains a number of pairs of complex-conjugate poles, and a zero (simple antiresonance) at zero frequency. Each pair of complex conjugate poles comprises a resonance of the vocal tract, and is often referred to as a vocal tract “formant.”

An inverse-filter would have a complex zero for every complex pole of the vocal tract in the frequency range of interest, and in addition, a pole or simple resonance at zero frequency. The primary limitations inherent in this method are as follows:

(1) The volume velocity waveform is indicated only up to an additive constant, i.e., there is no indication of zero flow.

(2) The method is highly susceptible to low-frequency noise.

(3) Amplitude calibration is difficult.

(4) A low-frequency error component is introduced by the air displaced by the movements of the articulators.

(5) The method requires a knowledge of the resonances of the supraglottal vocal tract for setting the parameters of the inverse-filter. Dynamically varying filter parameters are required during running speech.

(6) Errors are introduced whenever the mathematical model assumed for the supraglottal vocal tract does not accurately reflect the actual acoustic characteristics. In particular, the model specified above does not take into account nasalization.

The first two limitations stem from the fact that the inverse-filter requires a pole at zero frequency, which would be an integrator in the time domain. Since the initial conditions for the integrator are not known, the zero level of the waveform is lost. In practice, a true integrator cannot be used, and the pole is placed near, and not at, zero frequency. The first-mentioned limitation is important in that it means that periods of glottal closure (zero air flow) can only be inferred, as by using the relative flatness of the waveform as a guide. In addition, slow variations of average air flow, as when the voicing becomes breathy during an intervocalic /h/ in English, would not be recorded reliably. The sensitivity to low-frequency room noise is due to the increase in the low-frequency response of the filter caused by the pole near zero frequency.

Amplitude calibration, the third problem area, is difficult because it depends on an accurate and stable placement and orientation of the microphone with respect to the mouth.

The fourth source of error is due to the fact that the volume velocity being measured by inverse-filtering includes a component due to articulatory movements. For example, if we assume that a jaw movement displaces an average area of 12 cm², a very fast movement of the jaw, say 1 cm in 0.1 sec, would cause an average flow rate of 0.12 liter/sec. Using the pneumotachograph mask to be described below, the air flow during jaw opening movements of about 0.5 cm, repeated at a rate of about 20 per sec, while mimicking exaggerated productions of /babab–/, was found to be about 0.08 liter/sec peak and about 0.15 liter/sec peak to peak. The glottis was held closed during the test by maintaining a sizeable subglottal pressure. This type of error is not a problem in held vowels, or with vowels placed in a test frame designed for minimum articulatory movement (as directly following an /h/ in English).

The measurement of vocal tract resonances, the fifth problem area, has been discussed at length in the literature. Many of the methods in use are reviewed by Flanagan [9]. Some problems in measuring the resonances of the supraglottal vocal tract are discussed in this paper.

I. INVERSE FILTERING OF VOLUME VELOCITY

In the method discussed in this paper, the glottal volume velocity waveform during non-nasalized and slightly nasalized vowels is obtained by inverse-filtering the volume velocity waveform at the mouth (oral volume velocity) instead of the pressure waveform. The oral volume velocity is recorded by means of a specially constructed circumferentially vented pneumotachograph mask. An inverse-filter for the oral volume velocity waveform does not contain the integrator required for inverse-filtering pressure, with its attendant disadvantages outlined above (Nos. 1 and 2). In particular, inverse-filtered volume velocity provides a reliable indication of zero flow (except for the component due to articulatory movement), and is not susceptible to low-frequency room noise. The amplitude calibration problem (No. 3 above) is also not present when inverse-filtering volume velocity, because the mask measures the total air flow from the mouth and nose, which is the same as the glottal air flow at low frequencies, and it can be easily calibrated by a constant air flow. It might be noted that the integrator is also eliminated when inverse-filtering the particle velocity at some point in space instead of the volume velocity, however, the calibration problem would remain.

The major inherent deficiencies in this method that have been detected so far are the remaining limitations associated with the inverse-filtering of pressure, namely, Nos. 4, 5, and 6 in the preceding section. An important practical deficiency, when compared to the inverse-filtering of radiated pressure, is the difficulty of constructing some form of “pneumotachograph” transducer for measuring the volume velocity at the mouth that is accurate over the entire frequency range of interest in voiced speech. Because of this we can expect that any practical system for inverse-filtering volume velocity would have a limited frequency response. (This is not necessarily true for a system inverse-filtering particle velocity.)

A pneumotachograph transducer for measuring the volume velocity at the mouth must integrate the normal component of air flow over some topological surface enclosing the mouth. If the output of a pneumotachograph is to be used for inverse-filtering, it must satisfy the following criteria:

(1) The air flow resistance should be so low that there is a negligible disturbance of the pressures and air flows in speech.

(2) The output must be a linear function of volume velocity.

(3) There should be little distortion of the radiated acoustic signal.

(4) The response time of the pneumotachograph should be small compared to a glottal period.

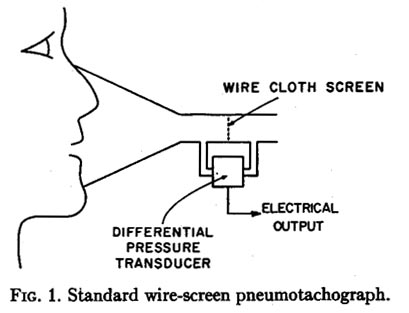
Shown in Figure 1 is a device used for some time in the study of respiration, termed the wire-screen pneumotachograph. The volume velocity of the breath stream is channeled through a layer of fine-mesh stainless-steel wire cloth. The pressure drop across the screen is proportional to flow over a wide range, and can be recorded by means of a differential pressure transducer.

Though this type of pneumotachograph normally satisfies criteria (1) and (2), the standard pneumotachograph mask greatly distorts the radiated acoustic signal and has internal resonances that limit unacceptably the available response time of the pneumotachograph.

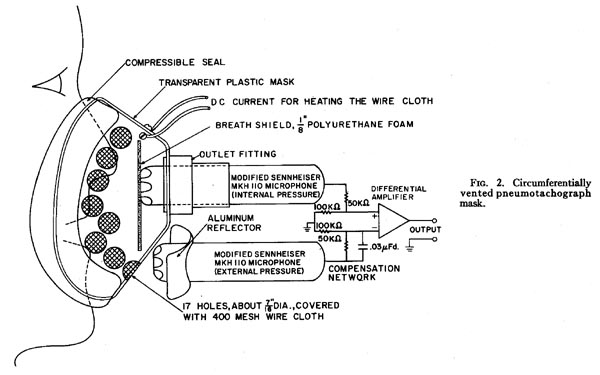
Covering the mouth and nose with a mask having a relatively high acoustic impedance adversely affects speech intelligibility in two ways, namely, by changing the natural frequencies (poles and zeros) of the vocal tract (the “loading” effect) and by filtering the resulting (distorted) speech (the “transmission” effect). The change in speech quality caused by the acoustic loading of a mouth enclosure was investigated as early as 1947 by Morrow [10,11].  Morrow differentiated between “radiating” and “nonradiating” enclosures. A pneumotachograph mask would normally be considered a radiating enclosure. The radiating enclosure analyzed by Morrow was coupled to outside air by a hole at the far end, as was the mask illustrated in Figure 1, and tended to lower the resonant frequencies of the vocal tract, since it increased the effective length of the resonating system.

We have found that the effect of a radiating enclosure on the vocal tract resonant frequencies is greatly reduced if the coupling to the outside air is placed around the circumference of the enclosure, as close to the mouth as possible, instead of at the far end as assumed by Morrow. This type of radiating enclosure could be termed “circumferentially vented.”

The circumferentially vented pneumotachograph mask used presently by this laboratory is illustrated in Figure 2. The novel design feature is the distribution of the wire screen outlet around the circumference of the mask, as close to the mouth as practical. This placement minimizes the distortion of the acoustic resonances of the vocal tract, satisfying requirement 3. When placed close to the mouth, the relatively low impedance at the wire screen is acoustically in parallel with the much higher impedance of the remainder of the mask. In this situation, the principles of linear system theory dictate that the net impedance seen by the mouth is then approximately the impedance at the wire screen.

Because the wire screen is on the surface of the mask and not enclosed within a tube, this design minimizes the acoustic resonances in the pneumotachograph response, improving the acoustic-transmission characteristics as well as reducing the response time of the pneumotachograph (requirement 4).

Since the total volume velocity at any instant is the sum of the components passing through each hole, the volume velocity should ideally be measured by summing the outputs of 17 miniature differential pressure transducers located at each of the holes in the mask. However, this approach was judged to be impractical at present, owing to the lack of a commercially available differential pressure transducer that was small enough for this purpose, while having a sufficient sensitivity (full scale pressure about 0.5 cm H₂0) and a sufficiently broad frequency response (from 0 Hz to at least 1 or 2 kHz). Because of this practical limitation, we decided to use only one differential pressure transducer, located as centrally as possible. A mask with one transducer would be limited in response time, or frequency response, by the time required for a sudden pressure change at the mouth to be distributed throughout the mask. With the speed of sound about 1ft/msec, and the maximum mask dimensions on the order of 3 in., the response time of a one-transducer mask would be limited to about 1/4 msec. The equivalent frequency-response limitation is about 2 kHz. (A system of this type having a frequency response flat to some frequency f must have a response time of less than about 1/2f.) In other words, we can assume that the air flow components through the various holes, when averaged over 1/4 msec, were approximately equal, and could be measured by one centrally located transducer.

The pressure transducer used for the measurements reported here was a differentially connected pair of Sennheiser condenser microphones having a response down to zero frequency. The acoustic system of each microphone required some modification in order to make the response flat in the range 0-10 Hz. (The acoustic system of this microphone was not originally designed for operation in that range.) A disk of 1/8-inch thick polyurethane foam shielded the internal microphone from the direct impact of the breath stream. Without such a shield, it was found that the response of the pneumotachograph was not linearly related to air flow, and highly dependent on the shape of the mouth opening.

One problem with the microphone arrangement was that the outside microphone tended to have an output that was too low, due to the spreading of the pressure wave as it emerged from the mask. Merely increasing the gain for the outside microphone had the adverse effect of unbalancing the differential-transducer system with respect to ambient-noise cancellation. However, since the ambient noise was mostly at low frequencies, and the desired microphone signal mostly at high frequencies (since the outside microphone signal is roughly the time derivative of the volume velocity), it was found that increasing the high frequency gain by means of the network of four resistors and a capacitor shown in Fig. 2 could largely correct for the spreading of the pressure wave, while retaining effective noise cancellation. The aluminum reflector shown in Fig. 2 for the outside microphone was also helpful in increasing the microphone output while retaining noise cancellation. The parameters of the reflector and the RC filter were selected by trial and error to reduce the response time of the mask from about 1 msec without correction to just under 1/2 msec with correction. In this procedure the parameters of the reflector and RC filter were varied while observing the response to an impulse of volume velocity. The system for generating the impulse is described below. Since it was felt that 1/2 msec was within a factor of two from the shortest response time attainable with a one-transducer mask of this size, no further attempt was made to correct the output of the outside microphone using less ad hoc methods.

The type A Bennett respiratory mask was found to be quite handy for mask construction. The normal outlet was refitted to hold the internal microphone, and the outlet replaced with holes drilled circumferentially, as close to the mouth as possible. The rubber-covered, compressible face seal of the Bennett mask provides a good seal, with considerable jaw mobility.

The outlet holes were covered with 400-mesh stainless wire cloth, cemented in place. The wire cloth was fabricated as a continuous strip so that an electrical current could be applied conveniently, for heating the screen to prevent moisture condensation. One-half ampere dc was found sufficient to heat the screen to above body temperature. It was not certain that the heating of the wire screen is always necessary with a circumferentially vented mask, since moisture condensation is not as much a problem as in the standard pneumotachograph in which the wire screen is in a closed channel. However, to avoid errors from this source, 1/2 A was applied during all recordings.

Test data relating the mask in Fig. 2 to requirements 1-4 follow below.

A. Mask Resistance

In order to not disturb the pressures and air flows within the vocal tract, it is necessary that (1) the time constant RC, where R is the resistance of the mask and C is the compliance of the supraglottal cavity, be less than about 1 msec, and (2) the mask resistance be less than one-tenth the resistance of the glottis in its most open state in speech.

The maximum compliance for the supraglottal cavity found by Rothenberg [12] was 0.004 liter/cm H₂0. The maximum mask resistance, according to the first requirement, is then about 0.001/0.004 = 0.25 cm H₂0/liter per sec. This figure also approximately satisfies the second requirement. The mask now being used (Fig. 2), has a measured resistance of 0.30 cm H₂0/liter per sec (see Fig. 3). This value has also proven to yield a level of acoustic distortion that is acceptable for most speech measurements, as described below.

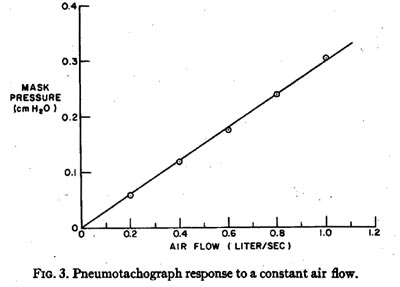
B. Linearity

The static-response curve is shown in Fig. 3. For this calibration, the air was directed through an orifice having the approximate shape of the lips open about 1/4 inch. Air flow was measured with a Manostat flowmeter having a rated accuracy of 0.03 liter/sec. Pressure was measured with the internal Sennheiser MKH110 microphone, calibrated against a Flow Corporation model MM3 micromanometer. Figure 3 shows that the response is linear to within the net 4% or 5% accuracy of the calibration instrumentation. Linearity probably extends to at least 1.35 liter per sec (the limit of the internal microphone) but measurements were limited to 1 liter/sec by the range of the flowmeter.

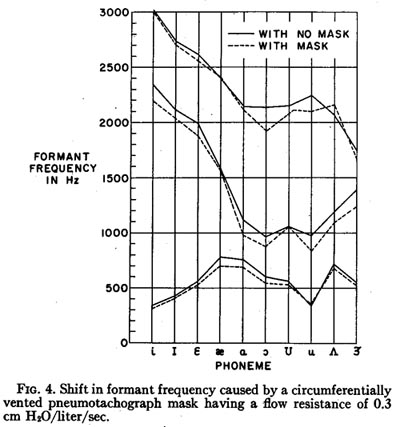
C. Acoustic Distortion

To test for the extent of the shift of formant frequencies caused by the loading of the mask, a male adult English-speaking subject recorded repetitions of the test frame /'hVd/ (“a heed,” “a hid,” etc.) with the vowel /V/ ranging over all the nonglided English vowel phonemes. The series was repeated with no mask and with the mask in place. The microphone was located outside the mask, about 10 in. from the mouth. Both wide-band and narrow-band spectrograms were made of all utterances, with a Kay model 6061 spectrograph, and the first three formant frequencies measured at a point just after the /h/, where a steady-state vowel articulation could usually be found. Figure 4 shows the average of the wide-band and narrow-band measurements. The measurements shown in this figure can be considered to have a standard deviation of less than 25 Hz and an absolute accuracy of better than 5%. As expected, most formants are slightly lower with the mask in place, due to the increase in the effective length of the vocal tract. No comparison with a standard pneumotachograph mask is shown, since with a standard mask the distortion is so severe that most formants above the first cannot be reliably identified.

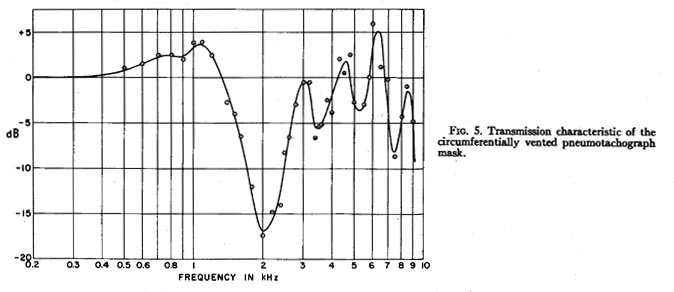
The transmission characteristic (frequency response) of the mask is also of interest, in that it affects the speaker’s perception of his or her voice, and, therefore, the naturalness of the resulting speech. The transmission characteristic of the mask was measured using a sinusoidal volume velocity source within the mask, and a microphone about 2 ft from the mask, in an anechoic chamber. The transmission characteristic shown in Fig. 5 represents the ratio, in decibels, of the microphone signal with the mask in place to the microphone signal with the mask removed. It can be seen that within the speech range the attenuation caused by the mask is within ± 6 dB except for a pronounced dip between about 1600 to 2600 Hz. For adult speakers, the primary result of this dip is an attenuation of the third formant, and in some cases, the second. Unlike the distortion due to a shift in formant frequency (Fig. 4), this distortion could conceivably be attenuated by some form of acoustic or electroacoustic compensation filter, however for most applications the acoustic effect is not sufficient to warrant such compensation. Though one can hear the effect of the mask, all vowels and consonants are clearly identifiable.

D. Response Time

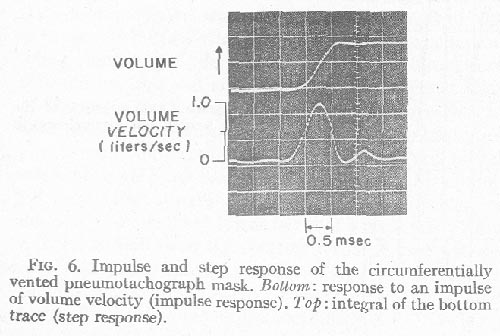
Figure 6 shows that the response time of the pneumotachograph for the mask we have been using is about 1/2 msec, which is equivalent to a frequency response limitation of about 1000 Hz. The lower trace in Fig. 6 shows the impulse response of the mask. The input to the mask was a mechanically generated volume velocity impulse with a duration of less than 1/2 msec. It was generated by passing compressed air through a slot in a rotating disk. The disk was 6 inches in diameter and had a number of slots roughly 2 mm X 3 mm, located radially, about 1 inch from the periphery. The disk rotated between the end of a tube supplying pressure at about 15 psi and a small fixed slot, 1 mm ´ 3 mm, leading into the mask at the location a mouth would be at, through a fixture molded to the contours of a face for the purpose of holding the mask. The slots on the disk were small enough so that the source impedance was high compared to that of the mask. The duration of the impulse was reduced by increasing the speed of rotation of the disk until no briefer impulse-like waveform could be obtained. A 6-pole linear-phase low-pass filter having a 1/2 amplitude (– 6 dB) frequency of 870 Hz was used to remove unwanted higher-frequency components. The step response in the upper trace was obtained by integrating the impulse response displayed in the lower trace. Higher settings of the low-pass filter resulted in a faster response, with progressively more overshoot and ringing in the step response. When used in the measurement of inverse-filtered volume velocity, the total low-pass filtering in the system was roughly equivalent to a linear-phase filter with a response down 6 dB at about 1100 or 1200 Hz, and so the response time would be somewhat under 1/2 msec, with an overshoot of up to 4% or 5% possible near waveform variations approaching a step function.

A response time of 1/2 msec should provide a reasonable resolution of the shape of the glottal waveform for fundamental frequencies up to about 200 Hz, if it is kept in mind that fine detail in the waveform resulting from energy above about 1000 Hz is not present. The 200-Hz limit on fundamental frequency includes the normal speaking range of most adult male speakers, but is somewhat inadequate for most female speakers and for children.

E. Inverse-Filter Design

Since the pneumotachograph that was used limited the frequency response of the system to about 1000 Hz, the inverse-filter need only be matched to the vocal tract for that range of frequencies. Since the third formant of an open vowel is always well above 1000 Hz, the filter we used contains only two pairs of complex-conjugate zeros, to be adjusted to match the lowest two formants. Since a practical filter must have more poles than zeros (so that the frequency response goes to zero as f ® ¥ ), each pair of complex zeros was synthesized with an associated three-pole low-pass filter of the Paynter configuration [13] having a – 3 dB frequency above the range of interest (at 1500 Hz for F₁ and at 2000 Hz for F₂). The Paynter configuration was chosen because of its linear phase response and its low overshoot and ringing.

The effects in the frequency range of interest of the third and higher formants were removed by a fixed, three-pole low-pass filter. The parameters of this filter were selected experimentally to approximately compensate for the effect of a third formant between about 2 and 3 kHz. The poles of the low-pass filter were chosen so that when cascaded with a pole pair representing the third formant, having a frequency anywhere between 2200 and 2800 Hz, the overall response was flat to about 1200 Hz and the step response had little or no overshoot. The resulting pole configuration of the filter was approximately that by Paynter (as cited above), with a gain of – 3 dB at 1000 Hz. A second setting, – 3 dB at 1300 Hz, was available for female speakers and older children, but was not used for the data reported in this study. The net effect of all low-pass filtering was to limit the response time of the inverse-filter to about 0.35 msec, and to introduce a time delay of about 0.7 msec.

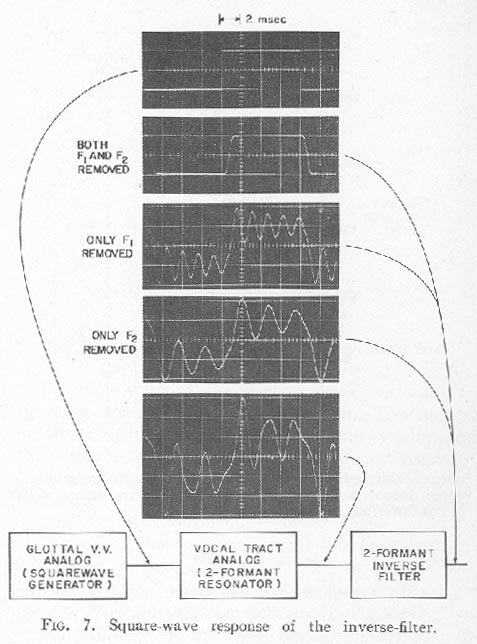
Some test results are shown in Fig. 7. The resonances in Fig. 7 were produced with an electronic two-formant vowel synthesizer. The filter compensating for higher formants was not used during this test. As can be seen in the output waveform of the filter with both formants removed, overshoot and ringing in the step response are less than 3%.

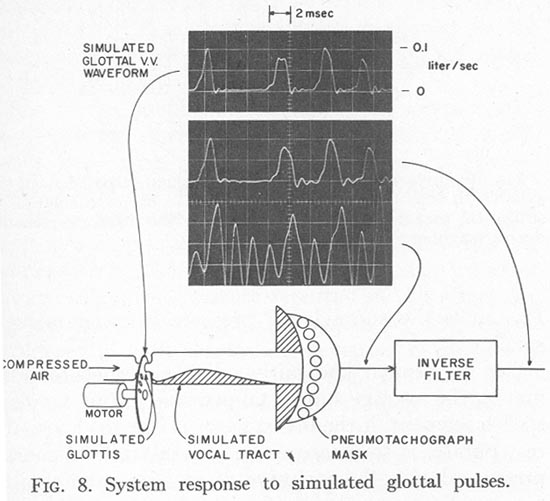
A simulated vocal tract was constructed so that the resonances could be produced acoustically, when used with the mechanical volume velocity generator (glottal air flow simulator) described above. By using the mechanical vocal tract, the accuracy of the entire system was tested, including the pneumotachograph mask and the compensator for the third and higher formants. A typical test result using this method is shown in Fig. 8. The volume velocity at the simulated glottis was recorded by means of a pressure transducer which measured the pressure behind a calibrated flow resistance in the air path, at the point at which the air enters the vocal tract. This flow resistance was composed of five layers of 400-mesh wire cloth, each about 0.3 cm² in area. To isolate the transducer from the vocal tract, this resistance was chosen to be over 100 times that of the mask, and at least 10 times the highest impedance of the vocal tract in the frequency range of interest.

The simulated glottal pulses shown in Fig. 8 were formed by a sequence of slots in the rotating disk having a variety of shapes and spacing. The resulting pulses represent a range of shapes and widths that might be found at the upper limit of the range of fundamental frequency for which this system was designed, or about 200 to 250 Hz. It can be seen that the system can reproduce the general shape of the glottal waveform with some fidelity even at this upper limit. The fidelity increased when the disk of the simulated glottis was rotated more slowly, to simulate pulses with a lower fundamental frequency. Five to ten percent of the inverse-filter output in Fig. 8 represents noise generated by the mechanism of the simulated glottis, and is not found when inverse-filtering human speech.

As a further test of the operation of the complete pneumotachograph, inverse-filter system in the higher frequency range of its response capability, the inverse-filtered volume velocity waveform was compared with the inverse-filtered pressure waveform. For this comparison, the upper limit on the frequency response of the pressure-derived waveform was limited to approximately that of the volume velocity system. It was necessary to use a natural, spoken vowel for this test, since the noise level produced by the mechanical glottis of the artificial vocal tract was too high for the inverse-filtering of pressure.

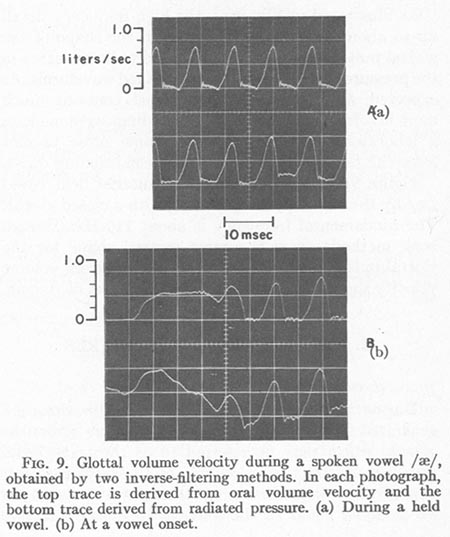
A typical result is shown in Fig. 9(a) for a segment of a held vowel /æ/ produced by an adult male speaker at a level somewhat louder than average. The fundamental frequency was 125 Hz. The upper trace was the inverse-filtered volume velocity waveform, and the lower trace the inverse-filtered pressure waveform. The same inverse-filter, at the same settings for formant frequency and damping, was used for both traces, except that an RC integrator with a time constant of 25 msec was added in the pressure channel, to approximate the additional pole at zero frequency required when inverse-filtering pressure. The procedure used for setting the inverse-filter parameters is described below. The pressure waveform was obtained from the outside microphone of the pneumotachograph mask. The volume velocity and pressure waveforms were recorded on an FM instrumentation tape recorder, inverse-filtered while being reproduced individually from a tape loop, and photographed from a Tektronix model 564 storage Oscilloscope. Time synchronization between the traces was maintained by triggering the oscilloscope from an impulse on the tape loop, and was accurate to within 1/2 msec. Since there was no natural calibration for the amplitude of the pressure-derived waveform, it was set to approximately match the amplitude of the calibrated, flow-derived waveform.

As illustrated in Fig. 9(a), the high-frequency detail up to about 1000 Hz, as reflected in the shape of the glottal pulses, was consistently found to be the same in the pressure-derived and the flow-derived waveforms. As expected, the pressure-derived signal contains much more low-frequency noise. The recordings were made in a laboratory environment, with some noise present from the tape recorder and the air conditioning ducts.

Figure 9(b) shows the onset of another held vowel /æ/ by the same speaker, starting with a closed glottis. The fundamental frequency is about 110 Hz. Though both methods show the same general shape for the glottal pulses, only the waveform derived from volume velocity shows clearly the nature of the onset of voicing.

II. EXPERIMENTAL PROCEDURES

A. Subglottal Pressure

During voiced speech, the laryngeal vibrations are generated from the difference in air pressure across the glottis, which may be referred to as the transglottal pressure. During the production of all except the most constricted vowels, the average transglottal pressure can be assumed equal to the average subglottal pressure P_sg, since the supraglottal pressure is comparatively small.

One convenient and fairly reliable method for estimating the average subglottal pressure during a voiced speech segment, if the investigator is free to choose the test phrase, is to measure the supraglottal (intraoral) pressure during the occlusion of an adjacent unvoiced plosive. For example, if the vowel to be used is the English /a/, the subject could be instructed to say “hop” (/hap/). During the closure of the /p/, the supraglottal pressure can be measured via a small tube at the corner of the mouth. It can be shown that due to the slow rate-of-change for “active” (respiratory muscle activated) changes in respiratory muscle tension, the subglottal pressure during the /p/ will usually be close to the average subglottal pressure during the preceding /a/. [12] The error due to the active variation in subglottal pressure can be minimized by embedding the test vowel between two /p/ phonemes, and extrapolating between plosives, as illustrated below.

Another source of error in this method is the “passive” decrease in subglottal pressure due to the air flow during the vowel. The average pressure drop during the vowel that is due to the air flow can be computed, given some rough estimates of certain subglottal parameters. The required parameters are the total effective subglottal flow resistance and the net subglottal tissue compliance. [12] However, the effect of the “discharge” of the tissue compliance can be largely compensated by embedding the test vowel between two /p/ phonemes and extrapolating between the oral closures. (Embedding a vowel between plosives also increases the likelihood of the vowel being non-nasalized, a factor important when using inverse-filtering.)

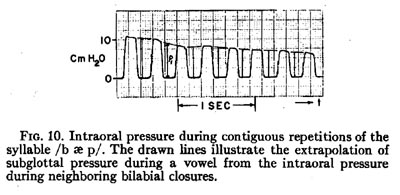
All estimates of average subglottal pressure reported in this paper were obtained by this method of extrapolating supraglottal pressure. The details of the method used are illustrated in Fig. 10. The vertical lines are drawn at the times at which the glottal waveform was sampled during each repetition of the syllable /b æ p/. At each vertical line, an extrapolated pressure P₁ is obtained from the intraoral pressure during neighboring lip closures. By using a double consonant sequence /pb/ between vowels, instead of a single /p/, the high air flow in the aspiration of the /p/ is avoided. When extrapolating pressure between pressure pulses, care was taken to neglect any decrease in pressure just before the bilabial release that could be attributed to the closing of the vocal folds in preparation for the voiced release of the /b/.

Due to the subglottal resistance, the average subglottal pressure during the vowel is probably about 3% to 5% lower than the extrapolated value P₁. For example, an average air flow of 0.15 liter per sec and a typical subglottal resistance of 2.0 cm H₂0/liter per sec would result in a drop in average pressure of 0.3 cm H₂0. To compensate for the error due to air flow, the values of average subglottal pressure reported in this study are 3% less than the extrapolated values P₁, and can be considered to have a standard deviation of about 5% for samples of non-breathy voicing, and may be as much as 7% or 8% high for the samples of breathy voicing.

To measure intraoral pressure during the bilabial closures, a curved plastic tube, 5/64 inch inside diameter, was fitted into the pneumotachograph mask so as to enter the corner of the mouth when the mask was in place. The tube led to a Pitron type PT-2 pressure transducer having a linear range of about 40 cm H₂0. Total path length from the end of the plastic tube within the mouth to the Pitron transducer element was about 1³/₄ inches. The transducer was calibrated against a water manometer. The frequency response of the system was flat to well beyond the range of interest (about 0-50 Hz) and was not measured directly.

B. Recording and Reproducing Procedures

An FM instrumentation tape recorder was used to record the air flow and oral pressure waveforms, and the radiated acoustic pressure signal, as obtained from the external microphone of the pneumotachograph. Inverse-filtering was accomplished while reproducing the tape-recorded air flow waveform. The inverse-filtered waveform was then recorded on a second recorder at 30 in./sec, with the unfiltered air flow waveform and the acoustic and oral pressure waveforms simultaneously rerecorded on other tracks.

For visual inspection and measurement, the waveforms were traced on a hot-wire oscillograph having a response flat to about 75 Hz. By operating the second recorder at 1/32 real time when reproducing signals for the oscillograph, the equivalent frequency response of the oscillograph was increased to 2400 Hz.

C. Inverse-Filter Adjustment

Initial estimates for the frequency settings of the inverse-filter were determined by measuring the first two formant frequencies on narrow-band spectrograms made on a Kay spectrum analyzer, model 6061A. When the vowel of interest was in a /b vowel p/ context, the formant frequencies were measured at a relatively steady-state portion, usually roughly 40 or 50 msec after the release of the /b/. For each sequence of /b vowel p/ syllables, the formants were measured on a representative set of syllables through the sequence. The measurements were checked for a drift in vowel articulation, as sometimes occurred when the pitch or loudness was varied during the sequence. Not all syllables were measured, since in the analysis procedure it was inconvenient to reset the filter frequencies for each syllable. For each sequence, an average or typical value was determined for each formant frequency, though if the formant measurements varied more than about 10% or 15% within the sequence, the sequence was divided into two or three subsequences, and typical formant values determined for each subsequence.

In some cases, the formant frequency controls were readjusted slightly (by no more than 10%) to minimize the oscillations at the formant frequency during the flat portion of the glottal waveform, which represents the most closed portion of the glottal cycle. The theoretical justification for this procedure is discussed later, in Sec. IV.

Estimates of the formant damping were obtained from the oral volume velocity waveform by measuring the cycle-to-cycle decay in the oscillation at the formant frequency which occurred just after the sharp decrease in air flow caused by the closing of the glottis. The relation between the percent decay per cycle and the damping factor δ is given by

where d is defined as the constant in the damping term of the Laplace transform expression for one formant (pair of complex poles):

               1               
(σ/jω_n)² + 2δ(σ/jω_n) + 1

The radian frequency ω_n is the distance of the poles from the origin. The damping coefficient σ, representing the displacement of the poles from the jω axis is related to δ by

For formant bandwidths small compared to the formant frequency, the bandwidth (between –3 dB frequencies) is approximately linearly related to the damping factor:

The decay per cycle was found to vary between about 20% and 40% for all non-breathy productions. The equivalent range of damping factor, from Eq. 1, is 0.04 to 0.08. Thus the formant bandwidth for F_l, assuming an average formant frequency of 650 Hz, varied between about 52 to 104 Hz. Values of damping in this range are slightly higher than those reported by House and Stevens [14] and Fujimura and Lindqvist [15], probably due to the energy absorbed by the mask.

It was found possible to use one average value of damping, say 30% decay/cycle, for inverse-filtering waveforms of the type reported in this paper. When the first formant was more than three or four times the fundamental frequency, it was found that varying the damping controls between 20% and 40% decay/cycle produced little change in the inverse-filtered waveform.

III. EXPERIMENTAL RESULTS

All inverse-filtered volume velocity waveforms reported below were taken from productions of contiguous syllables /b vowel p/, where the vowel was either /a/ or /æ/. The high first formant during these vowels makes the setting of the inverse-filter less critical. [4] The examples were selected from some 300 syllables that were produced and analyzed, about two-thirds from speaker P.B. and one-third from speaker M.R. Both speakers were adult males.

Sequences were produced in which the speakers attempted to vary primarily the subglottal pressure, keeping the laryngeal adjustment approximately constant, or attempted to vary fundamental frequency, keeping the subglottal pressure approximately constant. In some of the sequences an attempt was made to use a type of voice quality other than normal, as by using an especially high or low larynx position, or by trying to vary the degree to which the vocal folds were compressed. The speakers were required to monitor auditorily and kinesthetically their own subglottal pressure, laryngeal frequency, and voice quality, though instrumental feedback was sometimes used during practice sessions. The examples shown below were chosen as illustrative. To facilitate comparisons, the examples were mostly taken from one speaker, P.B. To insure a negligible error due to the frequencyresponse limitation of the mask, examples are shown only of vocalizations with a fundamental frequency below about 125 Hz.

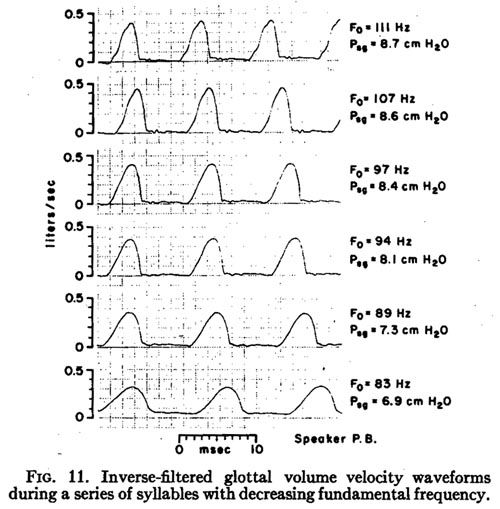
Figure 11 shows waveforms from six consecutive syllables of a sequence of syllables /bap/ produced with a decreasing fundamental frequency. Though the subject was attempting to hold subglottal pressure constant, there was some decrease in pressure during this subsequence, as shown in the figure. The average fundamental frequency for this subject during natural speech was roughly 105 to 110 Hz.

From a consideration of the various patterns of glottal movement that could have caused the offset from zero of the flat (most closed) portion of the lowermost waveform in Fig. 11, it is likely that the offset is due to an incomplete closure of the vocal folds posteriorly, between the arytenoid cartiledges, and might be termed interarytenoidal leakage. This lack of interarytenoidal closure in non-breathy voicing can be seen clearly in some of the motion pictures of the glottis taken by Moore et al [16].

Figure 12 shows typical waveforms selected from a series of syllables /b æ p/, produced this time with an increasing, then decreasing subglottal pressure. Though the fundamental frequency tended to vary in this sequence, it is likely that much of this variation was caused by the variation in subglottal pressure and not by a change in laryngeal adjustment. Hixon el al. [17], for example, report that in this voice register the fundamental frequency will vary between 2 and 3 Hz per cm H₂0, if the laryngeal adjustment is held constant. However, in the procedure used there was no direct control over laryngeal adjustment, and it cannot be assumed constant.

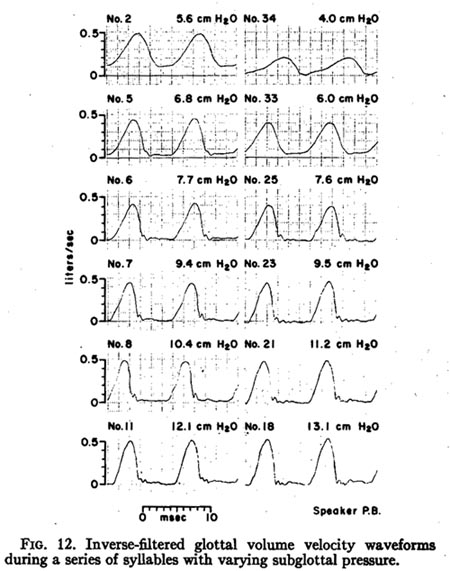
In discussing the waveforms in Fig. 12, and others following, it is desirable to separate occurrences of breathy and non-breathy voicing. We suggest the empirical definition that non-breathy voicing in the modal (chest) register be identified by an air flow waveform that has a marked flat or almost flat region, due to the coming together of all or part of the vocal folds, and that the minimum air flow be less than 10% or 15% of the peak air flow. For example, among the examples in Fig. 12, only the top-left waveform would be considered breathy.

It is interesting to note that the variation in the height of the non-breathy glottal pulses in the sequence used for Fig. 12 was approximately proportional to the variation in subglottal pressure. In other words, the peak glottal conductance (conductance defined as volume velocity divided by pressure) tended to remain constant for the non-breathy productions. In fact, a slight decrease in peak glottal conductance with increasing subglottal pressure, about 5% per cm H₂0, was generally observed in the sequences produced with varying loudness. (Some of the decrease in measured peak glottal conductance might be due to the smoothing of the recovered glottal pulse caused by the limited frequency response of the pneumotachograph. This effect would tend to be greater at higher subglottal pressures, where the true glottal pulse is more peaked. However, an examination of the recovered glottal pulse waveforms indicates that this effect could account for only a small proportion of the decrease.) It can be concluded, therefore, that the peak glottal area also tended to decrease slightly with increasing subglottal pressure in these sequences, since the peak glottal conductance can be considered a good measure of peak glottal area for the same, or similar, laryngeal adjustments.

The zero levels in the waveforms of Fig. 12 are only known to within about ±25 milliliters/sec. This estimate was arrived at by considering a number of factors affecting the zero level, the most important of which was the error due to air displaced by the movements of the supraglottal articulators. (A tolerance of roughly ±25 milliliters/sec could be assumed for the zero level of all examples presented in this paper, except for those in Fig. 11. Those in Fig. 11 were spoken more slowly, with a more pronounced steady state, and had a somewhat more accurate zero level.) This error is small when comparing peak air flows, but can result in inaccuracies of up to ±20% when measuring average air flow. However, even with this degree of error it can be seen from the waveforms in Fig. 12 that the average air flow increased very little with subglottal pressure-, though the peak air flow increased, the glottal pulses became narrower. The average volume velocity remained at roughly 150 milliliters/sec throughout the sequence. Thus the average glottal conductance decreased markedly with subglottal pressure.

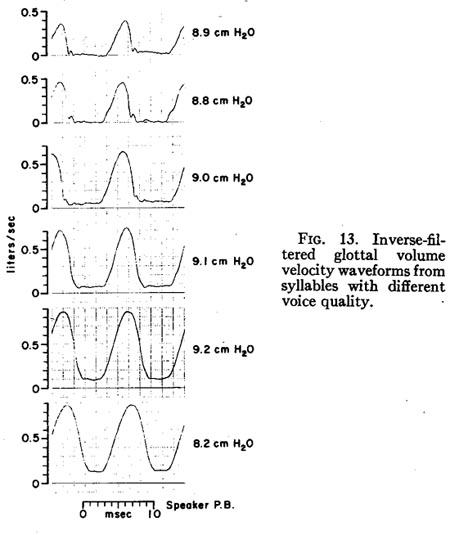
The values of glottal air flow and conductance for the examples in Figs. 11 and 12 represent rather typical values for this subject. However, as pointed out by Ladefoged and McKinney [18], the glottal conductance can vary over a wide range for any particular value of subglottal pressure. However, Ladefoged and McKinney measured only average air flow or conductance. It is also not clear to what extent their data include samples of breathy voicing. Our data verifies that peak glottal conductance can also vary over a range of at least about two to one, even if one excludes occurrences of breathy voicing. To illustrate this, we have assembled in Fig. 13 six examples of voicing produced with similar values of subglottal pressure (approximately 9 cm H₂0), that cover the range of peak glottal conductance found with this subject at that pressure. These examples were chosen from a total of four different sequences produced with different types of voice quality. According to our definition above, only the bottom-most waveform might be considered breathy voicing, with the second from the bottom being marginally non-breathy.

The second from the top was the most typical in size and shape for this speaker when trying to use a “normal” voice quality. It is from the sequence of syllables /b æ p/ used for Fig. 12.

The waveform at the top of Fig. 13 had one of the lowest values of peak conductance recorded for this subject in the context /b vowel p/ for a subglottal pressure of about 9 cm H₂0. However, it is likely that lower values of peak glottal conductance could be obtained in a transient state, as when momentarily compressing the vocal folds in an attempt to produce an intervocalic glottal stop in rapid speech. [19]

At some values of subglottal pressure, the compression of the vocal folds will not only reduce the peak glottal conductance, but will result in a type of voicing identified as “vocal fry”,  “laryngealized”,  or  “pulsed register.” [20-22] The middle trace in Fig. 14 shows an example of this type of voicing. The speaker was subject M.R. The waveforms in Fig. 14 were from a series of syllables /bap/ produced with decreasing loudness. The change in register of the middle trace occurred inadvertently as the subglottal pressure was reduced. The waveform shows the double-pulsing pattern that sometimes occurs in this type of voicing. Also shown in the figure are two samples of modal voicing that occurred in the same sequence of syllables, at slightly higher and lower subglottal pressures.

Figure 15 shows an example of the waveform during a type of voice break that was found to occur occasionally at the onset of voicing with both subjects P.B. and M.R., when the subglottal pressure was somewhat higher than average. The voicing began in a high-pitched breathy mode, which changed, after about 40 msec, to a non-breathy voice in the modal register. The suddenness of the transition between the two modes of oscillation of the vocal folds indicates that the laryngeal adjustment just preceding the transition was “bistable”, in the sense that it was capable of producing two different types of glottal action.

 IV. ACOUSTIC INTERACTION WITH THE GLOTTIS

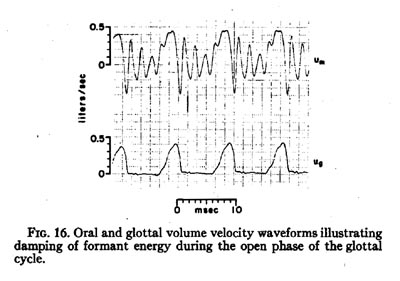
A decaying or damping of the formant frequency oscillations occurred consistently during the open phase of the glottal cycle, as shown in the waveforms of Fig. 16. The waveform of volume velocity at the mouth u_m shown in Fig. 16 was rather typical, and illustrates the manner in which the oscillations at the formant frequency decay much more abruptly as the glottis opens. The timing of the glottal opening and closing movements can be obtained from the waveform of glottal volume velocity, u_g, if one corrects for the delay of about 0.75 msec in u_g due to the low-pass filtering in the inverse-filter. By the time the next glottal closure occurs, there is virtually no remaining energy at the formant frequency. This decay of formant frequency energy during the open phase of the glottis is, at least in part, attributable to the increase in the damping of the resonances of the (glottal-supraglottal) vocal tract that occurs when the glottis opens [14, 15]. Let us consider what effect these changes in vocal tract acoustics have on the inverse-filtering process.

If one is interested in deriving the glottal volume velocity waveform (and not, for example, the glottal area waveform), the change in vocal tract acoustics caused by the interaction with the glottis does not actually cause an error in the inverse-filtering process, providing the inverse-filter parameters are set correctly, i.e., matched to the vocal tract acoustics with a closed glottis. However, the acoustic interaction between the glottis and the supraglottal vocal tract does make more difficult the determination of the proper inverse-filter settings. For example, a determination of the frequency and damping of the formants by an analysis of the radiated speech spectrum would not yield the correct values, if the spectrum is averaged over a time period including an interval during which the glottis was open (as is most often the case in spectrum analysis).

A spectrum analysis would be most accurate for inverse-filtering if averaged over only the most closed portion of the glottal cycle. This observation is a justification of the procedure proposed by Miller [4]  and Holmes [6], and used in the present investigation, of adjusting the inverse-filter parameters so as to remove the formant frequency oscillations during the flat, most-closed portion of the glottal cycle.

The acoustic interaction between the glottis and the supraglottal vocal tract is also significant when considering the relationship between the glottal volume velocity waveform and the glottal area waveform. Returning to Fig. 16, we can see that the glottal volume velocity waveform has an oscillatory perturbation during the opening phase of the glottis that represents energy at F₁ being absorbed at the glottis. This perturbation was undoubtedly caused by the change in vocal tract acoustics that occurred when the glottis opened, and is probably not found in the glottal area waveform, according to the model studies by Flanagan and Landgraf [23]. Lindqvist [8] has also noted this type of perturbation in glottal waveforms obtained by inversefiltering pressure, though at that time he hypothesized that it might be due to vibrations of the vocal folds caused by the acoustic variations in transglottal pressure.

The waveform in Fig. 16 was the topmost in the sequence of syllables /bap/ used for Fig. 11 above. If we compare this waveform with the others shown in Fig. 11, we note that as the fundamental frequency decreases, the inverse-filtered waveform appears to have less of this type of distortion, since the formant frequency oscillations die out to a greater degree before the glottis opens. The sequence of waveforms used for Fig. 11 were illustrative of a trend in the rest of the data, in that the perturbation in u_g due to the change in vocal tract acoustics during the glottal cycle, as evidenced by an “s-shaped” perturbation in the inversefiltered waveform during the opening phase of the glottis, tended to be negligible when the ratio of first formant frequency to fundamental frequency was more than about five or six.

There are probably other aspects of the glottal waveform that can be ascribed to the glottal-supraglottal acoustic interaction. For example, there may also be a significant effect on the waveform during a rapid closing of the glottis, since appreciable energy near F_l, produced by the closing of the vocal folds, may be present in the vocal tract before the vocal folds are closed.

V. DISPLACED GLOTTAL AIR

The simplified model of the glottal source proposed by Flanagan [2] assumes that the air flow into the glottis is always essentially equal to the air flow out of the glottis, i.e., no air flow is generated within the glottis. Air flow could be generated within the glottis if the compressibility of the enclosed air was a significant factor, however, this is not the case, as is pointed out by Flanagan.

A second possible source of volume velocity within the glottis is the air displaced by the movements of the glottal walls during the glottal cycle. A rough computation shows that this air flow component need not be negligible. For example, if we assume, after van den Berg et al. [1],  that an adult larynx adjusted for chest voice has glottal walls about 1.8 cm long by 0.3 cm high, for an area of 0.54 cm² , and that the maximum separation of the vocal folds during the glottal cycle was about 0.1 cm when averaged over the length of the glottis (from the area measurements of W. W. Fletcher, as reported by Flanagan), then the volume of air displaced each time the vocal folds open or close is about 0.05 milliliter. Again consulting the curves of glottal area presented by Flanagan (or the glottal volume velocity waveforms presented in this paper), it is possible to have an opening or closing of the vocal folds in the chest voice, or modal, register that takes place in as little as 2 msec. Dividing the displaced volume by time, we find that the average volume velocity during that glottal movement due to the displaced air would be 25 milliliters/sec. The peak flow might be two or three times that figure.

If we assume that the displaced air flows equally into the trachea and into the vocal tract, we can conclude that the movement of the vocal folds could add or subtract as much as 30 or 40 milliliters/sec from the glottal flow entering the vocal tract. This figure, though not large, is not insignificant.

The flow due to the displaced air would be subtracted from the volume velocity increase during the opening of the glottis, and added to the volume velocity decrease as the glottis closes. The effect of these added components would be to skew the volume velocity waveform to the right, by slowing down the increase of volume velocity during the opening phase of the glottis, and partially maintaining air flow during the closing phase, to make the decrease more abrupt.

The displaced air components may help explain why the glottal volume velocity waveforms obtained by inverse-filtering usually appear much more skewed or unsymmetrical than the area waveforms reported in the literature, and why the trailing (closing) edge of the glottal volume velocity pulse seems to fall off more sharply than would be predicted from just the nonlinearity of the glottal resistance and inertance parameters. Another factor that may help cause this difference between observed area and volume velocity may be the acoustic interaction discussed above between the glottis and the supraglottal vocal tract, as speculated by Miller [4].

The flow component due to displaced air may help explain some of the differences of voice quality that are noted when the vocal folds are widened vertically in the lower ranges of fundamental frequency.

At higher fundamental frequencies, the vocal folds generally become thinner, and the displaced air volume decreases. However, there is a simultaneous increase in the velocity of vocal fold movement, and so the volume velocity component due to the displaced air may still be significant.

ACKNOWLEDGMENTS

I wish to thank Paul R. Back for his assistance in the construction and testing of the inverse-filter and in data collection. This work was supported by a Public Health Service research grant from the National Institute of Neurological Diseases and Stroke.

REFERENCES

1.  J. W. van den Berg, J. T. Zantema, and P. Doornenbal, Jr., “On the Air Resistance and the Bernoulli Effect of the Human Larynx”,  J. Acoust. Soc. Am. 29, 626 (1957).

2.   J. L. Flanagan, “Some Properties of the Glottal Sound source”,  J. Speech Hear. Res. 1, 99 (1958).

3.  G. Fant, “The Acoustics of Speech”, Proc. III Int. Congr. Acoust., Stuttgart, Germany, 1959.

4.  R. L. Miller, “Nature of the Vocal Cord Wave”,   J. Acoust. Soc. Am. 31, 667 (1959).

5.  M. V. Mathews, J. E. Miller, and E. E. David, Jr., “An Accurate Estimate of the Glottal Waveshape”,  J. Acoust. Soc. Am. 33, 843 (1961).

6.  J. N. Holmes, “An Investigation of the Volume Velocity Waveform at the Larynx during Speech by Means of an Inverse Filter”, Proc. Speech Communication Seminar, Stockholm, 1962, Vol. 1, paper B-4 [Royal Institute of Technology, Stockholm, 1963].

7.  J. E. Miller and M. V. Mathews, “Investigation of the Glottal Waveshape by Automatic Inverse Filtering”,   J. Acoust. Soc. Am. 35, 1876 (1963).

8.  J. Lindqvist, “Studies of the Voice Source by Means of Inverse Filtering Technique”,  Congr. Rep. 5th Int. Congr. Acoust., Liège, 1965, Vol. 1, paper A35.

9.   J. L. Flanagan, Analysis Synthesis and Perception of Speech (Springer-Verlag, Berlin, 1972), 2nd ed.

10.   C. T. Morrow, “Reaction of Small Enclosures on the Human Voice, Part I, Specifications Required for Satisfactory Intelligibility”,  J. Acoust. Soc. Am. 19, 645 (1947).

11.  C. T. Morrow, “Reaction of Small Enclosures on the Human Voice, Part II, Analyses of Vowels”,   J. Acoust. Soc. Am. 20, 487 (1948).

12.  M. Rothenberg, The Breath-Stream Dynamics of Simple-Released-Plosive Production (Karger, Basel, 1968), Bibliotheca Phonetica VI. 

13.  P. D. Hansen, “New Approaches to the Design of Active Low-Pass Filters (Part II)”,  The Lightning Empiricist, 13, 3 (1965).

14.  A. S. House and K. N. Stevens, “Estimation of Formant Band Widths from Measurements of Transient Response of the Vocal Tract,” J. Speech Hear. Res. 1 (4), 309 (1958).

15.  O. Fujimura and J. Lindqvist, “Sweep-Tone Measurements of Vocal Tract Characteristics”,   J. Acoust. Soc. Am. 49, 541 (1971).

16.  G. P. Moore, F. D. White, and H. von Leden, “Ultra High-Speed Photography in Laryngeal Physiology”,  J. Speech Hear. Disord. 27, 165 (1962).

17. T. J. Hixon, D. H. Klatt, and J. Mead, “Influence of Forced Transglottal Pressure Changes on Vocal Fundamental Frequency”,  J. Acoust. Soc. Am. 49, 105 (1971).

18.  P. Ladefoged and N. P. McKinney, “Loudness, Sound Pressure and Subglottal Pressure in Speech”,  J. Acoust. Soc. Am. 35, 454 (1963).

19.  M. Rothenberg, “The Glottal Volume Velocity Waveform During Loose and Tight Glottal Adjustments”,    Proceedings VII International Congress on Phonetic Sciences, Montreal, August 22-28, 1971 (Mouton, The Hague, in press).

20.  H. Hollien, P. Moore, R. Wendahl  and J. Michel, “On the Nature of Vocal Fry”,  J. Speech Hear. Res. 9, 245 (1966).

21.  G. E. Peterson and J. E. Shoup, “A Physiological Theory of Phonetics”,  J. Speech Hear. Res. 9, 5 (1966).

22.  T. Murry and W. S. Brown, Jr., “Subglottal Air Pressure during Two Types of Vocal Activity: Vocal Fry and Modal Phonation”,  Folia Phoniatr. 23, 440 (1971).

23.  J. L. Flanagan and L. L. Landgraf, “Self Oscillating Source for Vocal Tract Synthesizers”,   IEEE Trans. Audio Electroacoust. 16, 57 (1968).

Home

Publications

E-mail

Papers online