An Interactive Model for the Voice Source*

by Martin Rothenberg**

Vocal Fold Physiology: Contemporary Research and Clinical Issues, D. M. Bless and J. H. Abbs, Eds., College Hill Press, San Diego, pp. 155-165, 1983.

A parametric model for the voice source is described which includes the acoustic interaction between the glottal source and the subglottal and supraglottal acoustic systems.

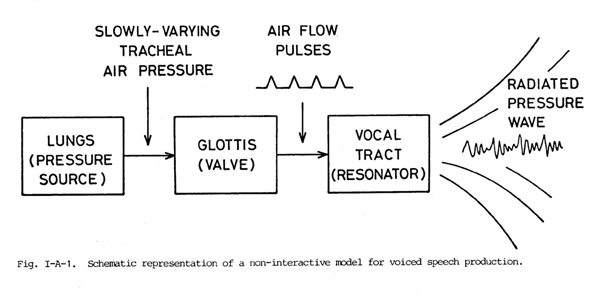
The acoustic theory of speech production, as first proposed, and as generally now implemented in formant-based speech synthesis, models the speech production mechanism during vocalic sounds with three relatively independent subsystems. These subsystems, shown diagrammatically in Fig. I-A-1, are (1) the respiratory system, which produces a slowly varying tracheal air pressure, (2) a time-varying glottal flow resistance (more properly, a complex impedance) whose valving action creates quasi-periodic air pulses, and (3) a supraglottal vocal tract that shapes the spectrum of the glottal flow pulses. Though each of these systems interacts with the other two systems to some degree, order-of-magnitude calculations, model studies and early measurements have indicated that for many applications it is sufficient to consider these three subsystems as operating independently, at least during voiced sounds with no strong supraglottal oral constriction (Fant, 1960; Flanagan, 1972).

However, as we look for more precise models of the voice source, whether this be for higher quality synthesis of speech or singing, or for the study of unusual or pathological voice qualities, it is necessary to return to an interactive model. Detailed physical-acoustic models of the subglottal systems have been proposed that can generate patterns of pressure and air flow that seem quite realistic (Flanagan & Landgraf, 1968; Mrayati & Guerin, 1976; Titze & Talkin, 1979). However, such detailed models often do not make clear which aspects of the interaction between the glottal source and vocal tract are most active in determining the quality of the voice. In order to understand the way in which voice quality is affected by the source-tract interaction it is desirable to formulate a model or models that break down this interaction into its more important and less important components, just as in acoustic phonetics the supraglottal vocal tract in non-nasalized vocalic speech is modeled by a number of resonances with varying degrees of importance (the "formants") and, in physiological phonetics, by a small number of minimally redundant jaw, tongue and lip parameters representing the major degrees of freedom of the supraglottal speech production mechanism.

It appears to this writer that no previous parametric model of this type has satisfactorily explained the variety among the glottal air flaw waveforms that have been found when inverse-filtering the air flow or pressure at the mouth, and the relationship of these waveforms to the relatively simple and invariant waveforms of projected glottal width or area (width or area as seen from directly above or below the glottis) that have been reported from photographic and photoglottographic measurements (for example, Colton & Estill, 1981; Farnsworth, 1940; Hildebrand, 1976*; Gall, et al., 1971; Harden, 1973; Hirano, et al., 1981; Holmes, 1963; Koster & Smith, 1970; Kitzing, 1977; Kitzing & Sonesson, 1974; Lindqvist, 1965 and 1970; Miller, 1959; Moore, et al., 1962; Rothenberg, 1973; Sonesson, 1960; Tanabe, et al., 1975; Timcke, et al., 1958 and 1959. Hildebrand, 1976, contains an extensive bibliography of optical measurements before 1976.). The reason for this seems to be that progress toward a satisfactorily explanatory parametric interactive model has been delayed by an underestimate of the effect of the acoustic reactance of the subglottal and supraglottal vocal tract at frequencies below the first formant. When to this factor is added the oscillatory energy in the lowest supraglottal and subglottal resonances that is carried over between glottal cycles, it is possible to construct a useful interactive model of the voice source having a relatively small number of physiologically-based parameters. Such a model is sketched in this paper.

The glottal air flow waveform could be considered independent of the subglottal and supraglottal systems if the pressures immediately above and below the glottis were relatively constant during the glottal cycle. But this is often not the case. It is surely not the case for voiced consonants, or those vowel sounds in which there is a supraglottal constriction strong enough to raise the average supraglottal pressure to an appreciable fraction of the lung pressure (as strongly palatalized or labialized vowels). In such cases, the dissipative or resistive portion of the impedance at the supraglottal constriction is no longer negligible with respect to the glottal flow resistance, and we also find that the frequency of the first formant becomes very low (approaching zero as the constriction approaches a complete closure. However, in this paper we concentrate on the development of a model which is valid for the more open vocalic sounds that comprise most of speech and singing. In such sounds the (dissipative) supraglottal flow resistance is small compared to the glottal flow resistance and the frequency of the first formant is appreciably greater than the voice fundamental frequency. Our studies of the glottal flow have indicated that for such unconstricted vocal tract configurations the influence of the vocal tract acoustics on the glottal flow waveform stems primarily from two factors. The first is the subglottal and supraglottal pressure variations caused by the inertive components of the subglottal and supraglottal vocal tract impedances at the voice fundamental frequency F0 and its lower harmonics, and the second is the supraglottal pressure oscillations at the lowest vocal tract resonance. The subglottal pressure oscillations at the lowest subglottal resonance may also be significant at the higher ranges of fundamental frequency used in singing and some types of speech, but this factor has not been included explicitly in our model.

When the ratio of the first formant frequency (f₁) to f₀ is high, say, more than about three, the formant energy carried over between glottal cycles is small enough so that the inertive loading tends to be the more significant factor, tilting the glottal flow pulse to the right, and causing the sharp slope discontinuity at the instant of glottal closure which generates most of higher frequency energy in voiced speech. This mechanism is illustrated diagrammatically in Fig. I-A-2. In the figure, the vocal tract is shown as a horizontal tube with a simple constriction representing the glottis, and the glottal area waveform represented by a roughly triangular pulse. This pulse is similar in shape to many recordings of projected glottal area (the area of the opening that would be seen from directly above or below the glottis) that have been made using photoglottographic techniques.

For the purpose of this simplified discussion, the glottal constriction can be thought of as a purely dissipative flow resistance which is inversely proportional to the glottal area. In addition, the acoustic impedance of the supraglottal and subglottal systems can be approximated by an inertive reactance at f₀ and those glottal harmonics falling below f₁ (for the supraglottal system) and below the lowest subglottal acoustic resonance (for the subglottal system). The justification for this simplified representation is that the supraglottal acoustic impedance as seen by the glottis is inertive for frequencies more than a few percent less than f₁ and the subglottal acoustic impedance as seen by the glottis also tends to be inertive for frequencies between the highest respiratory tissue resonance, which is of the order-of-magnitude of 10 Hz in adults (van den Berg, 1960), and the lowest acoustic resonance, which is roughly 300 to 400 Hz in adults. (van den Berg's calculations (1960) result in a resonance frequency near 300 Hz; however, the oscillations in some of the subglottal pressure recordings made by Koike (1981) show a resonance at about 400 Hz.)

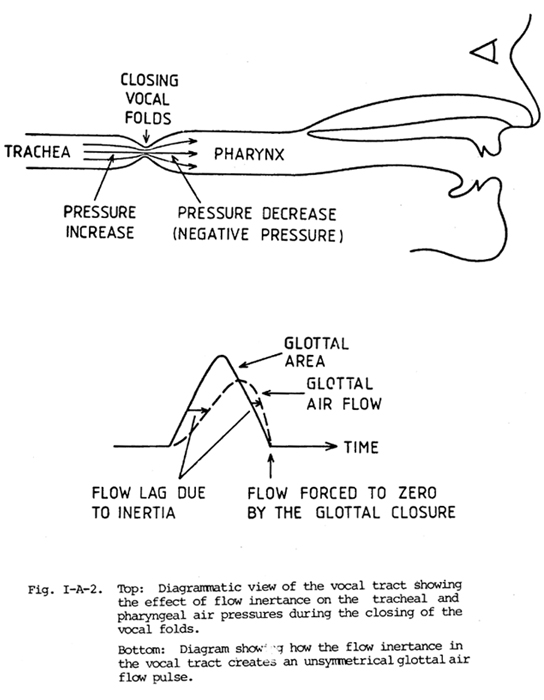
Since the subglottal and supraglottal air masses can be considered to be more inertive (mass-like) than compliant (compressible) under our assumptions, if the vocal folds open after being closed a long time, there will be a delay or lag in the build-up of air flow relative to the increase in area, as the lung pressure acts to overcome the inertia of the combined air mass. This lag is shown by the left-most horizontal arrow of the sketch of the glottal area and flow waveforms in Fig. I-A-2. (The inertance of the air mass in the glottis acts differently because it is time-varying and will be neglected in this simplified discussion.) If we assume a linear-system viewpoint, the opening phase of the glottal air flow, until about 3/4 of the glottal area pulse has passed, shows a time lag, or shift to the right, due to the time constant L_t/R_g, where L_t is the tract inertance at f₀ and its lowest harmonics and R_g is the (time-varying) glottal resistance. This time constant also causes an appreciable rounding or smoothing of the top of the air flow pulse, since the time constant is near its largest value at that time due to the low value of R_g.

However, the linear system analogy breaks down during the final 1/4 of the glottal pulse, since the closing vocal folds force the glottal resistance to be infinite at the closure (assuming perfect closure), and thereby force the flow to zero in a relatively short time. During that time interval (the last 1/4 or so of the glottal pulse) the tracheal pressure can be found to have a significant increase due to the inertance of the subglottal flow, and the pharyngeal pressure a significant decrease due to the inertance of the supraglottal flow (Kitzing & Lindqvist, 1975; Koike, 1981). Thus, the transglottal pressure during this interval is much higher than during the rest of the glottal pulse, and acts to support the glottal air flow until the actual instant of glottal closure is approached.

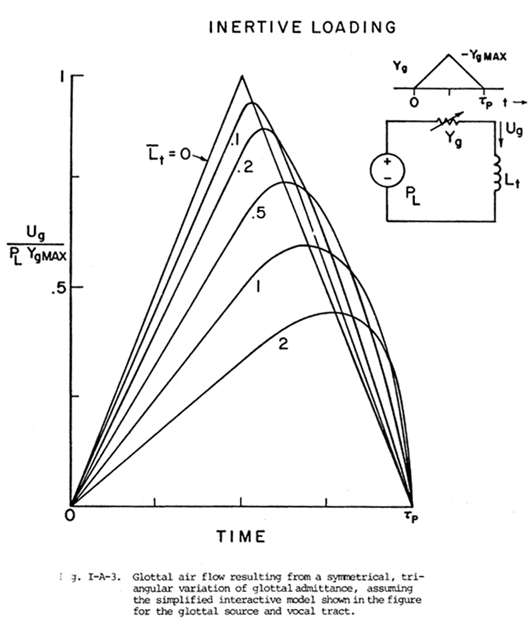
Fig. I-A-3 shows the solution of the nonlinear differential equation that results when the glottis is represented by a time-varying resistance and the subglottal and supraglottal acoustic systems by a single constant inertance (Rothenberg, 1981). The system is shown in the figure in its analogous electrical circuit form, where

The glottal flow conductance is assumed not to be flow dependent and to have a symmetrical triangular waveform, presumably from a roughly triangular area function. (It is shown in Rothenberg (1981) that the precise shape of the glottal conductance pulse does not materially affect the general properties of the solution of the nonlinear equation. The effect of flow dependence is discussed below.) The form of the resulting current pulse is determined by the "normalized vocal tract inertance" Lt defined as

where tp is the duration of the glottal pulse, and Y_gMAX is the maximum glottal conductance.

The major feature of the air flow waveforms in Fig. I-A-3 is that there is a critical range for the normalized inertance L_t from about 0.2 to 1.0, in which the glottal flow changes from a roughly symmetrical triangle to a rounded "sawtooth" having one major point of slope discontinuity at the instant of closure. In fact, the mathematical solution to this idealized case shows that the slope of the flow waveform becomes infinite at closure (as t®tp in Fig. I-A-3) for all values of L_t larger than unity.

Though we have not been able to find a closed form solution to the non-linear differential equation for the more realistic representation of Y_gin which Y_gdepends on U_g as discussed by Fant (1960) and Flanagan (1972), our experiments with an analog simulation of the differential equation, with and without flow dependence, indicate that the flow pattern with flow dependence included is similar to that without flow dependence if the value of L_t is decreased by about 50% when the flow dependence is removed. In other words, the flow patterns in Fig. I-A-3 can be used to predict the approximate flow pattern if an appropriate adjusted value of L_t is chosen.

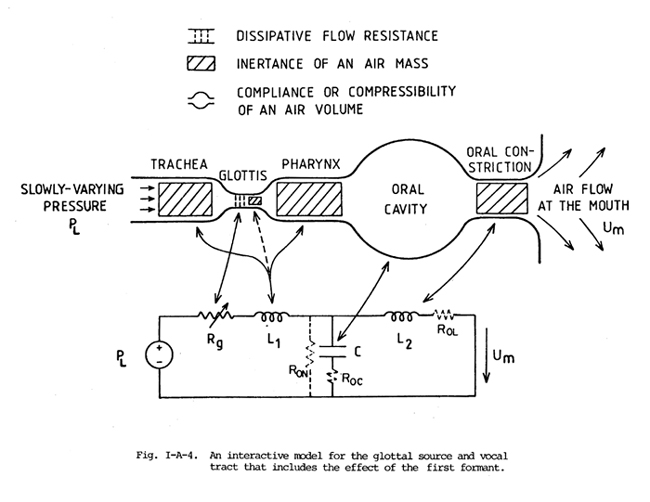
The R, L model in Fig. I-A-3 does not include the interaction with the first formant. To include a first-order approximation to the action of the first formant, the model can be modified by adding an oral compliance, C₀ as shown in Fig. I-A-4. This oral compliance can be considered a lumped approximation to the compressibility of the supraglottal air and, at lower values of f₁, a small component due to the effective compliance of the walls of the supraglottal tract. In this model, the supraglottal inertance is split into two parts, one on either side of the oral compliance. The forward or oral component is the prime determinant of f₁, in combination with C₀, while the rear or pharyngeal component is more important in determining the overall asymmetry or tilting of the glottal air flow waveform, since it acts directly on the glottis, without the "cushioning" effect of an intermediate compliance. In this model, a back vowel such as [a] would have a high value for the pharyngeal inertance and a low value for the oral component, while the reverse would hold for a front vowel such as [i]. Naturally, if this model is to be useful, a more detailed definition would have to be worked out from these general principles.

The dissipative elements associated with the vocal tract, R_OC,R_OL, and R_ON, are shown dashed, since not all may be needed in a simple model. R_OC primarily represents the dissipation associated with the compressibility of the air flow and the compliance of the cavity walls; R_OL represents the dissipation associated with the velocity of the air flow (boundary layer effects, etc,); and R_ON represents any shunting effects, such as a small velopharyngeal leakage. For non-nasal vowels with a high value of f₁, the main effect of oral dissipation is to determine the damping of f₁ during the period of glottal closure, and since the total dissipative loss is generally very small in this case, any one of these three components can be used. However, for low values of f₁ or for nasalized vowels, the placement and distribution of the dissipative loss elements should be reconsidered.

Informal experimentation with an electrical analog version of the model in Fig. I-A-4 has shown that as the ratio f₁/f₀ a gets smaller than about three, the value of this ratio is increasingly significant in determining voice quality. When f₁/f₀ is near integral values, energy from previous glottal cycles tends to cause a decrease in supraglottal pressure as the glottis is closing (in addition to any component caused by the low frequency vocal tract inertance). This decrease in pressure raises the transglottal pressure and, as discussed above, causes a sharper drop in flow at closure. Likewise, values of f₁/f₀ that fall about halfway between integral values tend to decrease transglottal pressure during glottal closure and cause a less sharp drop in flow at the instant of complete closure. Thus, if the ratio f₁/f₀ a is low, the high frequency energy generated by the glottal closure is determined by both the vocal tract inertance at low frequencies and the value of f₁.

The interaction between f₁ and f₀ should be differentiated from the interaction predicted by the linear, non-interactive model. In the linear model, a formant is maximally strengthened when it is an exact multiple of the fundamental frequency, while the value of f₁/f₀ for maximum transglottal pressure during the glottal closure may not be an exact integer. Of more significance is the fact that the linear non-interactive model predicts that the coincidence of f₁and a multiple of f₀ will strengthen only f₁ and not the higher order formants. The interactive model shows that the ratio of f₁ to f₀ can have a significant effect on all formants. This interaction between f₁ and the amplitude of the higher order formants was seen experimentally some time ago by Fant & Martony (1963), but, as they noted, it could not be justified in terms of a linear non-interactive model.

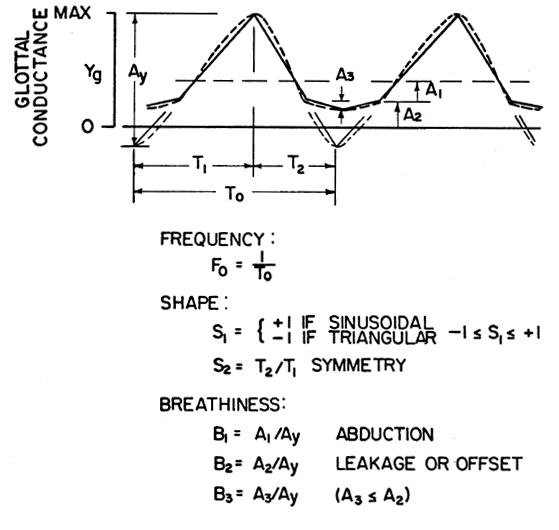Fig I-A-5

In Fig. I-A-4, the dashed line to the glottal inertance represents the fact that our testing of this model in its electrical analog version indicates that the effect of the time-varying glottal inertance is entirely different from the effect of the fixed vocal tract interance, and that the glottal inertance should be considered as a separate parameter with generally less significance than the fixed inertances L₁ and L₂. For the higher values of the ratio f₁/f₀ tested, the time-varying glottal inertance did not have much effect on the apparent value of L_t, as reflected in the asymmetry of the glottal flow pulse. Introduction of the glottal inertance merely caused a small reduction in pulse amplitude and a small added delay in the buildup of air flow, which reduced the discontinuity in the time derivative at the flow onset, thus producing a more gradual onset. (That a time-varying inertance should tend to act as a resistance and decrease the amplitude of the flow pulse is not so surprising if one considers that the time derivative of inertance has the sane units as resistance.)

What remains to be specified in the model are the parameters of the glottal resistance function R_g, or rather its inverse Y_g. Since, as noted above, a more realistic representation of the glottal resistance that includes flow dependence does not appear to be necessary if the value of L_t is adjusted appropriately, we model the glottal constriction by a linear conductance Y_g having a waveform illustrated in Fig. I-A-5 . The parameters of Y_g are as follows:

The open phase , with duration tp, is defined as the conductance "pulse" bounded by the discontinuities in slope at the head of arrow A₂. The closed phase is defined as T₀ - tp, and the duty cycle as tp/T₀. These are not considered independent parameters in this model, and can be computed from the values of f₀, S₁, S₂, B₁, and B₂.

Since the exact shape of the closed phase when A₃ and B₃ are non-zerois not very important, the form is assumed to follow the pattern defined by S₁. This assumption mat need reconsideration, however, since actual patterns of conductance variation during the closed phase, as estimated from flow measurements, vary widely and are not necessarily related to the form of the conductance variation during open phase.

Future work may indicate that other factors should be added to these glottal and vocal tract parameters, for example, an air flow component which is due to the air displaced by vocal fold motion and which appears to have a primary effect similar to a small increase in L_t (Rothenberg, 1973; Rothenberg & Zahorian, 1977; Flanagan & Ishizaka, 1978*). In addition, the effect of flow dependence on the conductance waveform should be specified more exactly, including a more explicit empirical definition of the value of the idealized (linear) parameter Y_g, that should be used to model an actual (flow dependent) glottal conductance. The effect of the time-varying glottal inertance at lower values of the ratio f₁/f₀ could be considered, and possibly the effect of f₂ when it is low in frequency. Also, a broader model should include a representation of the more significant dependencies between the parameters, as the dependency of A_yon P_L, U_g, and B₁.

Finally, I believe that an important part of any model for the voice source should be an ordering of the parameters according to their significance. At this point, I would estimate that the most basic parameters

are f₀, P_L, B₁, and A_L. That is, the proper specification of these parameters during running speech should allow a reasonably intelligible and natural-sounding foment synthesis, providing B₂, B₃, and C₀ are set to zero, and reasonably, constant values are chosen for L_t, S₁, and S₂.

For a more natural synthesis, I would estimate that L_t and B₂ should be dynamically varying, and perhaps C₀ should be added to include the interaction with the first formant. I would judge as least significant, but not necessarily always negligible, the effect of B₃, S₁, S₂and the air displaced by the moving vocal folds.

I could add in closing that this model leads naturally to some speculations as to the source of voice quality differences of glottal origin. If it is true, as inverse filtering results to date indicate, that some individuals have a glottal flow waveform that can be characterized as being generated with a higher or lower than average value of L_t, what parameter or parameters are responsible? The pulse duration tp (for a given f₀) can be such a factor; however, any attempt to voluntarily decrease tp by increasing the medial compression (adduction) of the vocal folds would also tend to decrease Y_gMAX, leaving Lt relatively unchanged. It is possible that a speaker with a voice naturally rich in harmonics may have a laryngeal configuration with an especially low Y_gMAX for a given tp , e.g. , vocal folds that open wider, or with a shape that results in a smaller resistance to air flow. Another possibility, of course, is a difference in the value of Lt due to the shape of the laryngeal vestibule or the characteristics of the jet of air emerging from the open glottis. Any component of Lt located that close to the glottis would have a maximal effect on the glottal flow waveform, while having a minimal effect on the frequencies of the vocal tract formants.

Acknowledgements
The model presented in this paper embodies a multitude of judgments about the relationship of the glottal flow waveform to certain underlying physiological parameters and the acoustic and perceptual significance of the resulting flow waveform differences. Most of these judgments are based on the author's experience with an analog simulation of the model that was constructed and tested while he was a guest researcher in the apartment of Speech Communication and Music Acoustics at the Royal Institute of Technology in Stockholm. During this period there was a constant interaction with staff members in the department, especially Professor Gunnar Fant and Dr. Jan Gauffin, and many aspects of the model reflect their comments, suggestions and questions. As one important example, I recall that it was during a discussion with Professor Fant that I first became aware of the potential significance in an interactive model of the subglottal component of the flow inertance and the subglottal resonances.

This work was sponsored, in part, by a grant from the U. S. National Institutes of Health and from the Bank of Sweden Tercentenary Foundation, grant no. 79-86.

References

COLTON, R.H. & ESTILL, J.A. (1981): "Elements of voice quality: Perceptual, acoustic and physiological aspects", in Speech and Language: Theory and Practice (ed. by N. Lass), Vol. 5, Academic Press, New York, pp. 311-403.

FANT, G. (1960): Acoustic Theory of Speech Production, Mouton, Hague.

FANT, G. & MARTONY, J. (1963): "Formant amplitude measurements", STL- QPSR 1/1963, pp. 1-5.

FARN, D.W. (1940): "High-speed motion pictures of the human vocal cords", Bell Lab. Record 18, pp. 203-208.

FLANAGAN, J.L. (1972): Analysis Synthesis and Perception of Speech, Springer Verlag, Berlin.

FLANAGAN, J.L. & ISHIZAKA, K. (1978): "Computer model to characterize the air volume displaced by the vibrating vocal cords", J .Acoust.Soc. Am. 63, pp. 1559-1565.

FLANAGAN, J.L. & LANDGRAF, L.L. (1968): "Self oscillating source for vocal tract synthesizers", IEEE Trans. Audio Electro-acoust. 16, pp. 57-64. -

GALL, B., GALL, D., & HANSON, J. (1971): "Larynx-Fotokymografie", Arch. klin.exp.Ohr-, Nas.- u. Kehlk.Heilk. 200, pp. 34-41.

HARDEN, R.J. (1973): "Comparison of glottal area changes as measured from ultrahigh-speed photographs and photoelectric glottographs", J. Speech and Hearing Res. 18, pp. 728-738.

HILDEBRAND, B.H. (1976): "Vibratory patterns of the human vocal cords during variations in frequency and intensity", Doctoral Diss., Univ. of Florida.

HIRANO, M., KAKITA, Y., KAWASAKI, H., GOULD, W.J., & IAMBIASE,A. (1981): "Data from high speed motion picture studies", in Vocal Fold Physiology (ed. by K.N. Stevens & M. Hirano), Univ. of Tokyo Press, pp.85-91.

HOIMES, J.N. (1963): "An investigation of the volume velocity waveform at the larynx during speech by means of an inverse filter", Proc. of the Speech Communication Seminar, Vol. I, Stockholm 1962, paper B-4. (Dept. of Speech Communication, Royal Inst. Technology, Stockholm).

KITZING, P. (1977): "Metode zur kombinierten photo- und elektroglottographischen Registrierung von Stinmlippenschwingungen", Folia Phoniat. 29, pp. 249-260.

KITZING, P. & LOFQVIST, A. (1975): "Subglottal and oral air pressures during phonation - preliminary investigation using a miniature transducer system", Medical and Biological Eng., Sept, 1975b, pp. 644-648.

KITZING, P. & SONESSON, B. (1974): "A photoglottographical study of the female vocal folds during phonation", Folia Phoniat. 26, pp. 138-149.

KOIKE, Y. (1981): "Sub- and supraglottal pressure variation during phonation", in" Vocal Fold Physiology (ed. by K.N. Stevens & M. Hirano), Univ. of Tokyo Press, pp. 181-189.

KOSTER, J-P. & SMITH, S. (1970): "Zur Interpretation elektrischer und photoelektrischer Glottograntre", Folia Phoniat. 22, pp. 92-99.

LINDQVIST, J. ( 1965) : "Studies of the voice source by means of inverse filtering technique", paper A35 in Congr.Rep. 5th la, Liege, Vol. 1.

LINDQVIST, J. (1970): "The voice source studied by means of inverse filtering", STL-QPSR 1/1970, pp. 3-9.

MILLER, R.L. (1959): "Nature of the vocal cord wave", J .Acoust. Soc.Am. 21-, pp. 667-679.

MOORE, G.P., WHITE, F.D., & von LEDEN, H. (1962): "Ultra high-speed photography in laryngeal physiology", J. Speech and Hearing Disorders 27, pp. 165-171. ,

MRAYATI, M. & GUERIN, B. (1976): "Etude de l'impedance d'entree du conduit vocal - Couplage source-conduit vocal", Acoustica 35. pp. 330-340.

ROTHENBERG M. (1973): "A new inverse-filtering technique for deriving the glottal air flow waveform during voicing", J. Acoust. Soc. Am. 53, pp. 1632-1645.

ROTHENBERG M. (1981): "Acoustic interaction between the glottal source and the vocal tract", in Vocal Fold Physiology (ed. by K.N. Stevens & M. Hirano, Univ. of Tokyo Press, pp. 305-323.

ROTHENBERG M. & ZAHORIAN, S. (1977): "nonlinear inverse filtering technique for estimating the glottal area waveform", J. Acoust. Soc. Am. 61, pp. 1063-1071.

SONESSON, B. (1960): "On the anatomy and vibratory pattern of the human vocal folds", Acta Oto-Laryng., Supple 156 (Lund).

TAKASUGI, R., NAKATSUI, M., & SUZUKI, J. (1970): "Observation of glottal waveform from speech waves", J. Acoust. Soc. Japan 26 (3), pp. 141-149.

TANABE, M., KITAJIMA, K., GOULD, W.J., & LAMBIASE, A. (1975): "Analysis of high-speed zrotion pictures of the vocal folds", Folia Phoniat. 27, pp. 77-87.

TIMCKE, R., von LEDEN, H., & MOORE, P. (1958): "laryngeal vibrations: measurements of the glottis wave, part I: The normal vibratory cycle", Arch. Otolaryng. 68, pp. 1-19, and part II: "Physiologic variations", Arch. Otolaryng. 69, pp. 438-444.

TITZE, I.R. & TALKIN, D.T. (1979): "A theoretical study of the effect of various laryngeal configurations on the acoustics of phonation", J. Acoust. Soc. Am. 66, pp. 60-74.

van den BERG, Jw. (1960): "An electrical analogue of the trachea, lungs and tissues", Acta Physiol. Pharnacol. Neer landica 9, pp. 361- 385.