Airflow-Based Analysis of Vocal Function
Published in: Vocal Fold Physiology: Acoustic, Perceptual, and Physiological Aspects of Voice Mechanisms, J. Gauffin and B. Hammerberg, Eds., Singular Publishing Group, San Diego, pp. 139-148, 1991.
Martin Rothenberg and Karen Nezelek
Dept. of Electrical and Computer Eng., Syracuse University, Syracuse. New York
13244. USA
One of the few noninvasive methods available for obtaining a clinically
useful estimate or description of the vibratory pattern of the vocal folds is
the inverse filtering of either the airflow or pressure waveform at the mouth
(Rothenberg, 1973, 1977), that is, the processing of the waveform at the mouth
with a filtering system that has a transform approximately the inverse of that
of the vocal tract between glottis and lips. For clinical purposes, inverse
filtering of the airflow at the mouth rather than the pressure is preferable,
since only the airflow method results in a known zero level and an easily calibrated
airflow scale for the resulting glottal flow waveform. The circumferentially-vented
wire-screen pneumotachograph mask has been shown to yield an oral volume velocity
waveform adequate for inverse-filtering up to about 1 kHz to 2 kHz, depending
on the mask configuration.
Though such a mask, combined with a manually-adjusted inverse filter, is now
being used by many voice research laboratories and a small number of research-oriented
clinical facilities, the necessity of properly adjusting the inverse filter
parameters for each subject - to match the frequency and damping of the lowest
one or two formants (vocal tract resonances) - makes this system impractical
for general clinical use. To overcome this problem, a number of laboratories
are attempting to develop computer-based, automated inverse filtering algorithms
(for example, Javkin, et al., 1987 and Gauffin, et al., 1986). Though of possible
value in the long term, presently proposed automated schemes can produce large
errors if the program errs. This is likely to occur for grossly abnormal voices,
such as highly breathy voices or in the presence of significant nasality. Both
of these conditions are counter to the assumptions upon which automated inverse-filtering
schemes are normally predicated. Sophisticated schemes for automated inverse-filtering
which are robust under a wide variety of voice conditions are yet to be developed.
This paper proposes a system for the airflow-based analysis of vocal function
employing a processing scheme for airflow signals that appears to bypass the
pitfalls inherent in standard inverse filtering and provide an easily used and
robust method for obtaining from the oral airflow waveform those parameters
of the glottal waveform having the most significance in clinical applications.
The method uses the output of a wide-band circumferentially-vented wire-screen
pneumotachograph mask during a spoken vowel having a high first formant, such
as /æ/ or /a/ in English, to derive a set of parameters adequate for reconstructing
a simplified or stylized version of the glottal waveform. These parameters are:
1. To, the fundamental period of each cycle
of the quasiperiodic flow waveform.
2. P, the peak airflow attained during each period To.
3. L, the minimum (lowest) airflow during each period. sometimes referred
to as the waveform offset from zero flow.
4. M, the mean or average airflow during each period.
5. Qo, often referred to as the open quotient, which is the
fraction of each period To during which the vocal folds are
essentially not in contact.
Each of these variables relates to physiologically significant variables of
clinical interest: (1) The importance of To as the primary
determinant of voice pitch is unquestioned. (2) For a given subglottal pressure.
the minimum now L indicates the degree to which the vocal folds do not
atlain a complele closure during the vibratory cycle. (3) The peak flow P,
or peak-to-peak flow P-L, would correlate well with the peak variation
in glottal area and, therefore, with vocal fold mobility and oscillalory efficiency,
assuming a given level of subgloltal pressure and ab-adductory force. (4) The
mean flow M determincs the rate of deflation of the lungs. (5) The open
quotient Qo tends to reflect the degree of abduction or adduction
of the vocal folds (as does P).
The proposed method is based on certain very general assumptions related to
the nature of glottal waveforms, namely, that (1) the primary excitation of
the vocal tract resonances for each glottal cycle occurs during thc glottal
closing phase, after the occurrence of the peak glottal flow. (2) the vocal
tract resonances are more highly damped during the open phase of the glottal
cycle, and (3) any strong wavefoml discontinuity in slope - most significantly
the abrupt flattening of the waveform caused by the closing of the vocal folds
over some portion of their length - will tend to occur near the smaller values
of instantaneous airflow rather than the higher values. These assumplions are
well supported in the literature and result from the basic physics of vocal
fold vibration and vocal tract acoustics. Finally, we assume that for the clinical
evaluation of vocal fold vibratory behaviour it is sufficient to record such
behaviour during an open vowel, such as /æ/ or /a/.
Under these assumptions, reasonable estimates of the peak and minimum values
of the glottal volume velocity waveform can be obtained by measuring the peak
and minimum values of low-pass filtered versions of the flow waveform at the
mouth. From the first two assumptions it can be inferred that there is little
formant energy added to the glottal flow by the vocal tract at the instant of
pcak glottal now; thc forrn:lnts would be slimulated just after the pcak now
for thc previous glottal cycle. and the resulting energy wouJd have largcly
decayed by the time that thc peak now occurs. since the peak flow occurs near,
usually just after the instant of maximum glottal area. (See for example Rothenberg,
1973, Figure 16, or Rothenberg, 1977, Figure 8). Thus, a small amount of smoothing
or low-pass filtering of the oral waveform, to further reduce formant energy
during the glottal open phase, should be sufficient to yield a waveform with
a peak value close to that of the glottal waveform. As we have previously shown,
a low-pass filter with good phase response and little or no ovcrshoot in its
transient response, such as a Bessel-derived filter, can be used for this purpose,
if the cutoff frequency of the filter is chosen to be above Fo but
significantly below the frequency of the first formant F1 (Rothenberg,
1977, Figure 8).
The minimum value of the glottal waveform is especially well retained by such
filtering, since, during the period of relatively constant glottal flow level
during a closed phase, there is time for the low-pass filter output to approach
this level. For wavefonns with little or no closed phase. The low-pass filtering,
as long as it is significantly above Fo, will still yield a reasonable
minimum value, since the Fourier component at Fo will tend to dominate
in both the oral and glottal waveforms.
We describe below two implementations of this procedure, as well as initial
test results for speakers having a variety of voice qualities. In the implementations
to be described. an approximate F1 inverse filter stage was added
to the low-pass filtering to increase accuracy with very strong voices, that
is, with voices having a relatively high amount of energy at the formant frequencies.
Method. first experiment
In our first experiment with the newly proposed method, we implemented an automatic
parameter measurement system of the type outlined and compared the resulting
parameter values with the values obtained by means of a standard inverse-filtering
procedure in which the filter parameters are manually adjusted by a trained
operator while observing the filtered waveform during a repetitive playback
of the voice sample. The system was tested with 29 subjects having a variety
of voice qualities.
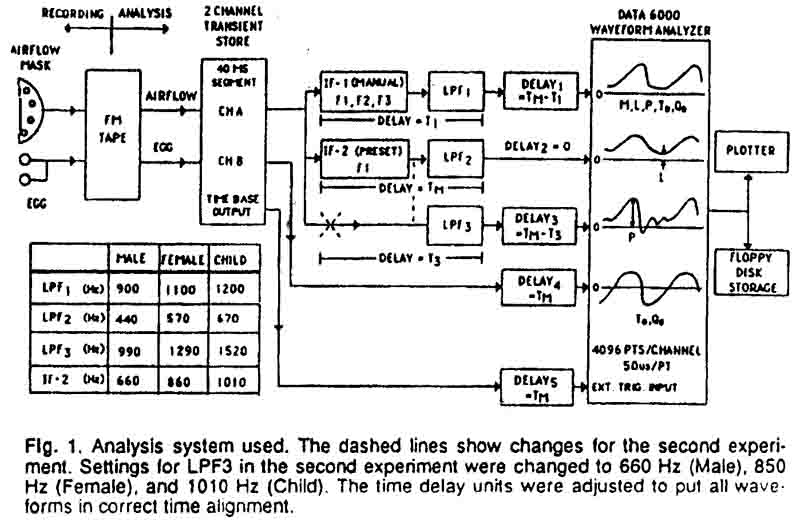
The test system was implemented on a Data Precision DATA 6000 microprocessor-based
waveform analyzer, with some of the signal filtering performed in analog form,
before A-D conversion. The system is shown in Figure 1. The output of an airflow
mask having a double layer of 500 mesh wire screen and a flow resistance of
about 0.5 cm H20/liter per second (Glottal
Enterprises model MA-2) and a Laryngograph electroglottograph were recorded
on FM tape. The electroglottograph signal was included to allow independent
measurements of To and Qo, though it was
realized that measurements of Qo derived from airflow and
EGG signal could be quite different. The EGG signal was also used occasionally
as an indication of the glottal closed period in setting the manual inverse
filter parameters (Rothenberg, 1979).
During analysis, a 40 msec segment of each vowel to be tested was first captured
on a two-channel, wide-bandwidth transient storage unit. This segment was then
recorded in the DATA 6000 signal analyzer in four forms:
(1) On Channel 1, a manually inverse-filtered glottal waveform was recorded,
using a standard analog filter (Glottal Enterprises model MSIF). Though four
formants could be removed by this filter, only three zero pairs (antiresonances
or antiformants) had any noticeable effect on the waveform for the voices tested.
(2) On Channel 2. an airflow signal was recorded that was passed through a single
formant approximate inverse filter set for the average first formant for the
vowel /æ/ for adult males, adult females or children, depending on the
subject, as taken from the classical study by Peterson and Barney (1952). The
anti formant (complex zero) damping factor was set to zero, though it was later
determined that a setting of about 0.5 in damping factor would have led to slightly
more accurate values of L in some cases. An 8-pole Bessel low-pass filler
with -3dB cutoff frequency set at 2/3 times the average formant frequency for
that subject category (Male, Female or Child) was also used to funher attenuate
the formant energy, as required by the proposed system design for estimating
the minimum glottal airflow parameter L. The Channel 2 signal was also
used by the DATA 6000 for estimating the waveform period To
and the mean airflow M.
(3) On Channel 3. the airflow waveform was only slightly low-pass filtered,
using an 8-pole Bessel filter set to -3dB at the relatively high value of 1.5
times the average F1 for the subject-age calcgory. According to the
system design, the maximum of this signal during To would
be used Cor estimating the peak glottal airflow P.
(4) The EGG waveform was recorded on Channel 4.

A program on the DATA 6000 automatically derived To,
M, L, P and Qo. To was measured at a
criterion level approximately half way between thc maximum and minimum values
of the captured sample in channel 2, and M was computed as the mean of
all data points in the channel 2 waveform during the period To,
L and P were measured according to the rules indicated in Figure
1.
The open quotient Qo was estimated from the airflow parameters
P, L and M by assuming a model for the glottal waveform
of a sinusoid truncated at its lower extreme. According to this model, Qo
is uniquely relaled to P, L and M by the equation:
sin(pQo) - pQocos(pQo)
/ 1 - cos(pQo) = pM
/ P - L
We found this equation to yield a reasonable first approximation for Qo,
given accurate estimates of P, L and M.
The system in Figure 1 was tested using 29 subjects as follows:
6 normal adult males
6 dysfunctional adult males
6 normal adult females
3 dysfunctional adult females
7 normal children (5 female and 2 male, 7 to 13 years old)
1 dysfunctional child (male, 11 years old).
The dysfunctional adults included cases of laryngitis, diplophonia secondary
to laryngitis, Parkinson's disease, post-surgery-trauma-induced left vocal fold
paralysis, trauma-induced breathiness, and simulated hyperfunctional-adducted
phonation. The child's vocal dysfunction was caused by a vocal fold nodule.
Each subject was asked to vocalize a short held /æ/ at a normal conversational
level, and at levels roughly 6dB above and below this level, as monitored by
the subject on a digital (LED) level display. The subject's most comfortable
pitch was used at each level. Twenty-eight subjects produced 3 loudness levels
and 1 subject produced 4 loudness levels, resulting in a total of 88 data points.
The manual inverse-filtering was performed by the second author or a graduate
research assistant, with each previously trained in this task by the first author.
Results. first experiment
We now consider the accuracy of the test system, using the manual inverse filter
result as a standard. We collapse our results across loudness, sex and age in
the following discussions, since scatter plots for the measures discussed indicated
that accuracy did not vary significantly wilh any of these variables, except
for a slight tendency toward more variability in the case of loud phonation.
Measurements of To in almost all cases showed differences
of less than two percent from measurements made from the EGG waveform. This
degree of accuracy would be expected from the results reportcd previously for
airflow-derived To measurements (Rothenberg, 1977). As would
also be expected measurements of mean airflow (M) made from the channel 2 signal
were essentially the same as those from the manually inverse filtered signal,
since the filtering procedures have no effect on the mean airflow. Qo
measurements roughly agreed with the predictions from the EGG signal. but no
quanlitative estimate of the correlation was derived, since the accuracy of
the flow-derived Qo would depend greatly on the accuracy of
the estimates of L and P.
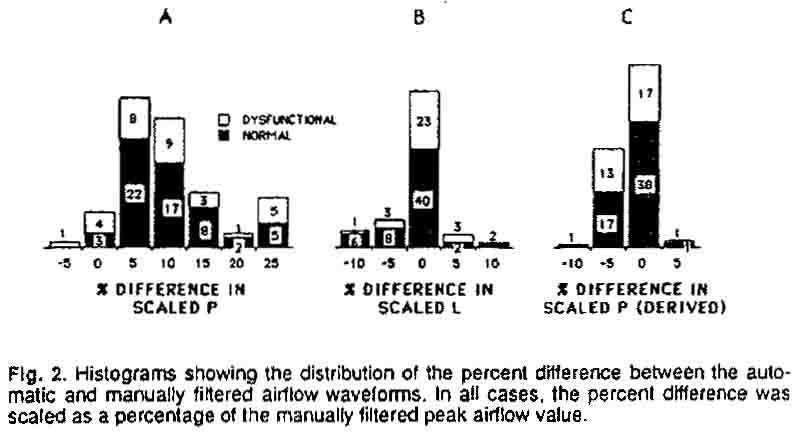
Thus, the parameters of most interest in these tests were the peak and minimum
values of airflow. In Figure 2A, the value of peak airflow P derived
by the automatic procedure (channel 3) is compared with the value obtained by
manual inverse filtering. The percentage error was computed assuming the manual
procedure to be the reference or accurate condition. It can be seen that the
errors were generally positive, resulting in values about 10% too high. This
error occurred for both normal and disordered voices.
As shown in Figure 2B, the error for the minimum value L was generally
less than 5%, with the automated procedurc tending to give values slightly less
than the manual filtering. As in Figure 2A, the percentage calculation was made
with reference to the peak value of the manually inverse-filtered waveform,
since this reference reflects the scale of interest for a particular waveform.
(Since minimum values can be very small, or even zero, using the more accurate
minimum value for the denominator would result in "error" percentages
with little meaning.) As with the peak values in Figure 2A, the accuracy was
generally maintained for both normal and disordered voices.
Interpretation - first experiment
The error in minimum value, about 5% of peak flow, with a maximum of about 10%,
would generally be considered adequate for clinical purposes. Variations of
much more than 10% can be found among normal voices of the same sex and age
and in a single voice within a sentence or at diffcrent times (Holmberg, el
al., 1988; Karlsson. 1988; Schutte, 1980). The tendency for this error to be
negative indicates that the errors may be largely due to remanent first formant
energy not removed by the automated filtering. This might explain why there
are proponionally more normal voices (with stronger F1 energy) that show the
higher errors. Thus, some increase in the strength of the low-pass filtering,
or a small reduction in the cutoff value, could conceivably reduce the error
further and remove the negative bias.
The error in peak value P was of somewhat more concern, though the errors shown
might still be acccptable for most applications. Because the error tended to
be positive (from the approximately filtered waveform exceeding the assumed
true glottal waveform), it was also deemed to be caused by some remanent F1
energy. This was verified by the data in Figure 2C, in which the peak of the
more highly filtered Channel 2 waveform was used as the test value. It can be
seen that the Channel 2 peak was generally within about 5 to10% of the accurately
filtered value, with a slight tendency toward a too negative value, as would
be caused by the overfiltering of the waveform. Thus, an optimum filter for
peak value would lie somewhere between those used for Channel 2 and Channel
3. This hypothesis was supported by the additional experiment to be described
below.
Thus, Figure 2 indicates that if the average error could be removed, an accuracy
of 10% when compared to actual peak airflow can be attained by the new automated
system in almost all cases, with most measurments within 5%. However, the presence
of a few outliers with possible errors of over 15% was disturbing, since a presumed
advantage of the new system was its robust procedure, that is, the absence of
any feature that could cause a large error in unusual cases. To probe this potential
problem further, a few of the outlying measurements were examined by comparing
the print-outs of the waveforms in each channel of the DATA 6000. In cach case,
the "error" was associated with a potentially incorrect manually inverse-filtered
waveform; the vocalization did not have the long. clearly defined closed phase
near zero flow that makes the inverse filter settings unambiguous. For example,
in some cases a detailed examination of the waveforms suggestcd that the Channel
2 low-pass filtered waveform better preserved the true minimum glottal flow
than did the presumably accurate, manually filtered waveform.
It therefore appeared to us that some significant proportion of the variance
in the "errors" reported in Figure 2 was, in actuality, caused by
errors in the parameters of the reference waveform. To investigate this possibility,
as well as to test a revised filtering procedure in Channcl 3 for measuring
P, as suggcstcd above, the following additional expcriment was performed.
Method - reevaluation experiment
In this second, reevaluation experiment, data from six of the original subjects,
chosen to represent the widest variety of glottal waveform types, were reprocessed
with the system revised as shown by the dashed lines in Figure 1. The same analysis
procedure was used, except that the manual inverse filtering for each sample
was performed independently by four members of the research staff. including
the two persons performing the previous inverse filter adjustments. Each adjuster
had extensive experience in this task.
In the reviscd system, the filtering for Channel 3 was altered to include the
approximate F1 inverse filter, and had a reduced low-pass setting, according
to our interpretation of the results in Figure 2, A and B, above. In addition,
the damping factor of the approximate Fl inverse-filter was changed from zero
to 0.5 to match the approximate average vocal tract damping with the mask in
place. The multiple versions of the manual inverse filtering were meant to give
some indication of the variability possible in the manually set antiformants
and the resulting variability in the reference values of P and L.
Results - reevaluation experiment.
Results from the second experiment indicated that the biases in the estimation
of both P and L are essentially removed in thc revised system.
An increased variability in the error values was found. since some of the more
difficult-to-inverse-filter voices were included in the sample of six subjects;
however, an appreciable part of this variability appeared to be due to inaccuracy
in the manual inverse filtering of the reference waveforms, as discussed above.
This conclusion is supported by the fact that thc highest error values generally
occurred with disordered voices that tended to be breathy. These waveforms usually
had no clear, flat "closed" period near zero now in the inverse-filtered
waveform to act as a reference in the adjustment procedure. In addition, informal
observations with other subjects confirmed that little variance between experimenters
is present when there is a clear closed phase with little or no airflow, as
was the case for our sample of a healthy male voice.
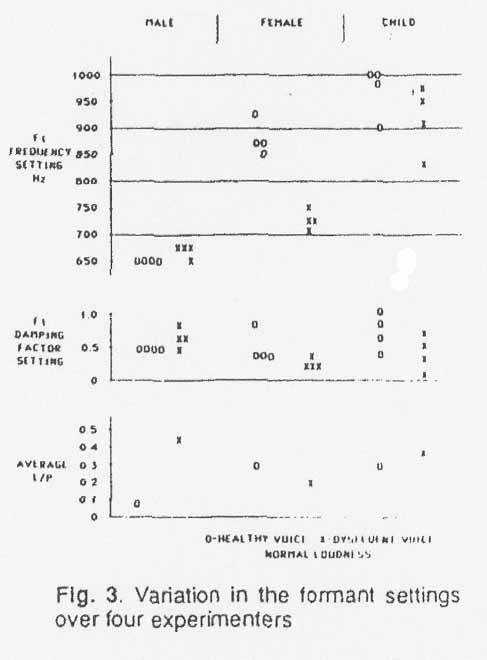
The variability in the formant settings for breathy voices is shown in Figure
3. The first-formant settings (the most significant formant in determining the
waveshape) are shown for all four experimenters for each of the six subjccts.
Also shown as a measure of relative breathiness is the ratio L/P,
as averaged over all reference values. This ratio will be zero if a complete
glotta1 closure is attained during the closed period and approaches unity for
very breathy voices. It appears from the figure that the variability in the
formant settings is to some extent correlated with this measure of breathiness.
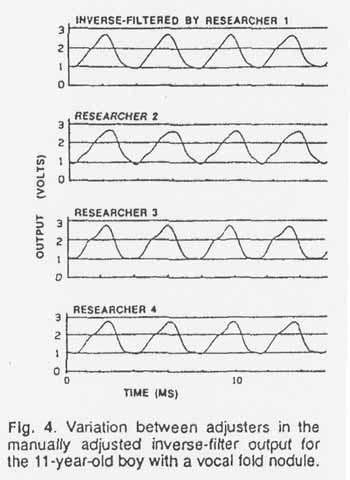
To show the effect on the waveform of the range of formant settings obtained
by the different adjusters. Figure 4 presents the manually inverse-filtered
waveforms from a vocalization by an 11-year-old boy diagnosed as having a vocal
nodule. Though the resulting waveforms are grossly the same, there would be
a significant variance in the resulting values for the minimum value L
and, to a lesser extent, for the peak value P. It should be emphasized
that without further knowledge there is no way to choose with confidence the
most accurate waveform among the four. Even a waveform that shows some residual
F1 energy near its minimum value could be correct, since there could be (and
probably is) some F1 energy passing through the open glottis during that time
interval.
Reconstructing Idealized Waveforms
The airflow-based analysis system we envision would print out for each subject,
in addition to the measured numerical parameter values, an idealized glottal
airflow waveform that conforms to these values. This type of graphical printout
would greatly simplify judgments of vocal function by making visually transparent
the interrelationship of the various parameters and would also facilitate intra-
and intersubject comparisons. In addition, when the analysis is performed separately
for a number of consecutive glottal cycles, the resulting reconstructed waveform
would exhibit more clearly the nature of any gross aperiodocities.
To test the viability of this type of graphical printout, the analysis results
from three of the subjects were transferred manually from thc DATA 6000 system
to a microcomputer which generated the required idealized waveform, given the
measured parameter values. To conform to the truncated sinusoidal approximation
of the glottal pulse described above, the idealized glottal volume-velocity
Ug is defined by
Ug = [P - L / (1 - cos(pQo)] * cos(2pt)/(To) + P - [P - L/(1 - cos(pQo)]
during the "open" periods, and remains at L during the "closed" periods. This equation results in a symmetrical waveform that has the required values of To, M, L, P, and Qo. To show a diversity of waveform types, the subjects chosen for this exercise were an adult male known to have a strong, efficient voice, the adult male Parkinson's disease patient, and the 7-year-old healthy female child.
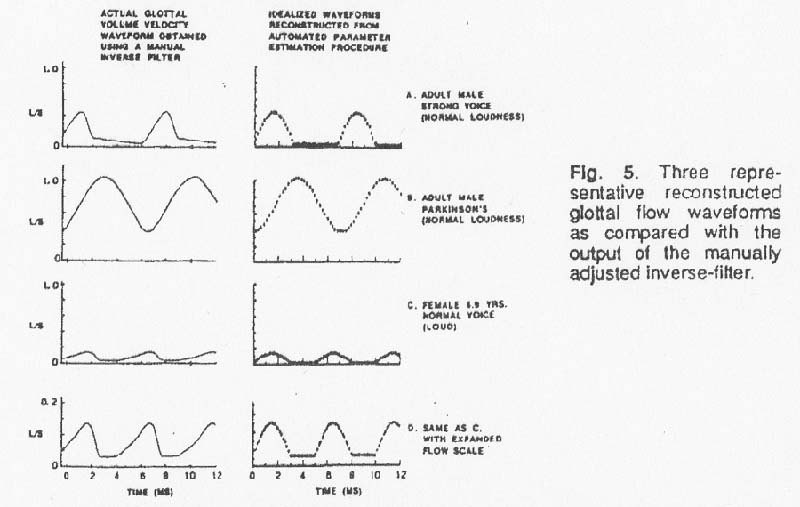
Parts A, B and C of Figure 5 compare the reconstructed glottal flow waveforms
with the output of the manually-adjusted inverse-filter. The child's waveform
is also shown with an enlarged flow scale, because of the much lower flow values.
It can be seen from the figure that the reconstructed waveforms retain most
of the significant properties of the manually obtained inverse-filtered waveforms,
while eliminating many of the details such as a slight closed-period slope or
remanent F1 energy - which would be of minimal interest to the clinician. The
most notable exception is the asymmetry, or skewing to the right, of the glottal
pulse that occurs in stronger voices; this is caused primarily by source-tract
acoustic interaction and does not directly reflect vocal fold movements. However,
if it is eventually found to be of interest clinically, this asymmetry could
be inserted into the idealized waveform and the corresponding computation of
Qo, using a simple model of a source-tract interaction such
as the one wruch was originally proposed by the author (Rothenberg, 1981) or
a similar model proposed by Fant (1983). A measure of spectral balance or spectral
slope for the mask waveform that reflected the relative strength of the higher
frequency harmonics could also be used to help determine the degree of asymmetry,
since a strengthening of the higher frequency harmonics is a primary correlate
of this asymmetry.
CONCLUSIONS
The results descrired above indicate that an automated parameter extraction
system, similar to our revised system can re constructed that will have a standard
deviation that is no more than 5% of the peak airflow value for measurements
of both the minimum and peak flow values. This system will be robust in that
it will rarely result in errors of more than about 10% of the peak flow value
when used according to the designated protocol (mask, seal adjusted for no leakage,
vowel similar to /æ/ or /a/). More precise determinations of system error
than those made in this project will be difficult to obtain without some independent
verification of the actual glottal airflow waveform that is more accurate than
manual inverse-filtering by a highly trained operator. There is no method now
available for such a verification in the human vocal tract, though a model experiment
(mechanical, animal or computer) might be possible.
However, as pointed out above, a variance of 5%, or even 10%, in the measured
values is not unreasonable for a clinical system. given the larger variance
found among normal voices or in the same voice at different times. The other
side of this coin must be that there are clinically significant variations in
these airflow parameters that exceed 5% to 10%. This is generally acknowledged
for average airflow, which has long been easy to measure, and evidence that
this is also true for the parameters of peak and minimum airflow is evolving
in current studies of breathy, hyperfunctional and aging voice (Fritzell, et
al., 1983; Hillman. et al., 1988; Higgins, 1989).
The extrapolation of Qo from M,
L and P also appears to be a reasonable alternative to other presently-proposed
noninvasive procedures for estimating this variable.
ACKNOWLEDGEMENTS
The research reported here was supported by Research Grant NS-08919 to Syracuse
University and by a Small Business Innovative Research (SBIR) Grant to Glottal
Enterprises, both from the National Institutes of Health. The measurements reported
were performed with the able assistance of Ashok Kalyanswamy, who was responsible
for the implementation and monitoring of the DATA 6000-based analysis system
and helped in the analysis procedure. Roy Thomas assisted in the design of the
microcomputer-based system used for Figure 5. Richard Molitor was the fourth
adjuster.
REFERENCES
Fant, G. (1983). Preliminaries to analysis of the human voice source. Speech
Communication Group Working Papers 3, (Research Laboratory of Electronics, Massachusetts
Institute of Technology).
Fritzell, B., Gauffm. J., Hammarberg. B., Karlsson, I.. and Sundberg, J. (1983).
Measuring insufficicnt vocal fold closure during phonation. STL-QPSR 4:50-59.
(Dept. of Speech Communication and Music Acoustics. Royal Institute of Technology,
Stockholm).
Gauffin. J., Hammarberg. B., and Imaizumi, S. (1986). A microcomputer based
system for acoustic analsyis of voice characteristics. Proc. ICASSP 86, Tokyo,
1:681-684.
Higgins, M. (1989). A Comparison of Selected Laryngeal Behaviors of Aged
and Young Adult Healthy Speakers. Unpublished doctoral dissertation. Syracuse
University, Syracuse.
Hillman. R., Holmberg, E., Perkell. J., Walsh. M., and Vaughan, C. (1988). Objective
assessment of vocal hyperfunction: an experimental framework and preliminary
results. Speech Commun. Group Working Papers. 6:67-135. (Res. Lab. ofElcclronics,
MlT)
Holmberg. E., Hillman. R.. and Perkell, J. (1988). Glottal airflow and transglottal
air pressure measurements for male and female speakers in soft, normal and loud
voice. J. Acoust. Soc. Amer. 84:511-519.
Javkin. H.R., Antonanzas-Barroso, N. and Maddieson, I. (1987). Digital inverse
filtering for linguistic research. J. Speech Hear. Res. 30:122-129.
Karlsson. I. (1988). Glottal waveform parameters for different speaker types.
STL-QPSR 2-3:61-63. (Dept. of Speech Communication and Music Acoustics, Royal
Institute of Technology, Stockholm).
Peterson. G. and Barney, H. (1952). Control methods used in a study of the vowels,
J. Acoust. Soc. Amer. 24:175-184.
Rothenberg. M. (1973). A new inverse-filtering technique for deriving the glottal
airflow wavefonn during voicing. J. Acoust. Soc. Amer. 53:1632-1645.
Rothenberg, M. (1977). Measurement of airflow in speech. J. Speech Hear.
Res. 20:155-176.
Rothenberg. M. (1979). Some relations between glottal airflow and vocal fold
contact area. Proceedings of the Conference on the Assessment of Vocal Pathology,
ASHA Reports 11: 88-96.
Rothenberg. M. (1981). Acoustic interaction between the glottal source and vocal
tract. In: Vocal Fold Physiology, edited by K.N. Stevens and H. Hirano, pp.
305-328. Tokyo Press, Tokyo.
Schutte, H. (1980). The Efficiency of Voice Production. Kemper, Groningen,
Netherlands.