Acoustic Interaction Between the Glottal Source and the Vocal Tract

Martin Rothenberg
Syracuse University
Syracuse, NY, USA

Vocal Fold Physiology, K, N. Stevens and M. Hirano, Eds., University of Tokyo Press, pp. 305-328, 1981
(Proceedings of the Vocal Fold Physiology Conference held in Kurume, Japan January 15-19, 1980.)

Of the possible causes for this flow dissymmetry, the following three appear to me to be the most likely to be significant:
(1) a non-invariant relationship between projected glottal area and glottal flow conductance (the reciprocal of flow resistance) due to the different vocal fold configurations that exist during the opening and closing phases,
(2) the small Component of air flow which is due to the air displaced by vocal fold motion (Rothenberg, 1973; Rothenberg and Zahorian, 1977),
(3) the effect of the supraglottal acoustic impedance.

The relationship between projected glottal area and flow conductance is likely to be significant in determining voice quality under some conditions. We will not consider this factor further in this paper, however, and we make the common first-approximation assumption that the relation between glottal conductance and projected glottal area is invariant.

Since the air displaced by vocal fold motion tends to decrease the glottal flow as the folds separate, and increase the flow as the folds come together (as in a hand clap), this component will tend to cause a dissymmetry of the type we are discussing. A simple calculation shows that the component will be small, but not necessarily negligible (Rothenberg, 1973. See also the simulation result by Flanagan and Ishizaka (1978).) However, in this paper we will not consider this component further, and we will study, instead, the effect of the third factor. We will consider the effect of supraglottal loading on the glottal waveform, using a model which is valid at the fundamental frequency and lowest order harmonics, since it is these components which most strongly influence the overall waveshape of the glottal pulse. Our comments will be restricted to acoustic interaction and not include the effect that the supraglottal pressure variations might have on the motion of the vocal folds.

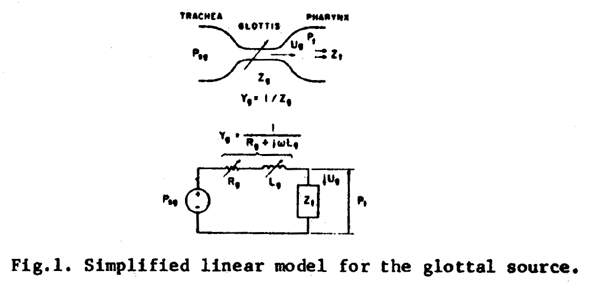
A MODEL FOR SOURCE-TRACT ACOUSTIC INTERACTION

Fig. 1 shows a simple linear. lumped-parameter model for the glottis and the supraglottal vocal tract. The elements in the model are in standard electrical circuit form, but are defined acoustically as follows:
Zg = glottal impedance (The dissipative part of the glottal impedance is termed the glottal resistance.)
Yg = glottal admittance (The dissipative part of the glottal admittance is termed the glottal conductance.)
Ug = glottal volume velocity
Psg = subglottal pressure
Zt = impedance of the supraglottal vocal tract as seen by the glottis
Pt = supraglottal pressure

In this paper. we will consider the subglottal pressure to be constant and the glottal inertance Lg to be zero. The glottal admittance will then be a pure conductance that is the inverse of the glottal resistance Rg and is equal to Ug/(Psg-Pt). In the following theoretical development, we will initially consider this admittance to have the symmetrical, triangular shape shown at the upper right in Fig. 2 as the vocal folds open and close during the glottal air pulse. Though this representation does not properly reflect the flow dependency of the glottal resistance (which for larger glottal areas causes the differential or small-signal flow resistance to be somewhat higher than the resistance defined by pressure/flow, and causes both measures of resistance to increase with volume velocity for a given glottal area), it should yield a good approximation to the actual glottal flow for small values of Zt, if the variation in projected glottal area is approximately triangular (Flanagan, 1958). In the common assumption of independence between the glottal source and the vocal tract, the supraglottal impedance Zt is considered negligible compared to Zg, and therefore, as shown in the curve for Rt = 0 in Fig. 2, the glottal air flow would have the same shape as the glottal admittance function Yg. In the figure, the pressure, admittance and time scales are normalized to arbitrary units (Psg = 1, Yg maximum = 1, pulsewidth = 2).

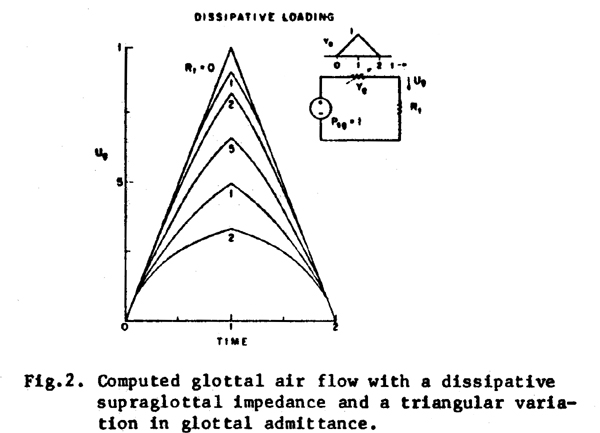
In looking at the effect of a non-negligible Zt, let us first assume Zt to be purely dissipative, as shown in Fig. 2, for some representative values of Rt. In this case, the air flow Ug is given by

At the initiation and termination of the air flow pulset Rg is high and dominates Rtt and the resulting flow is similar to that which would occur with no Rt. However, as Rg decreases (and Yg increases) the flow becomes limited by Rt. For high values of Rtt the flow Ug approaches a rectangular pulse of amplitude Psg/Rt, as it is "switched" on and off by the onset and offset of Yg. This rectangular pulse will have a much higher ratio of high-frequency energy to low-frequency energy than would be the case with Rt equal to zero (the non-interactive model).

A reactive supraglottal impedance will also cause an increase in the proportion of high frequency energy, The way in which this change occurs, however, is different from that for the dissipative case. If the lowest supra-glottal resonance (the first formant Fl) is higher than the voice fundamental frequency F0, as is usually the case, the supraglottal loading will be inertive at frequencies between F0 and F1. In addition, in a more accurate representation the inertive component of the glottal impedance would be added to the load impedance in determining the flow, thus increasing the importance of the effect of inertive loading. In this paper, we will present a mathematical analysis for only the case of an inertive reactance, assuming, for simplicity, that Zt is due to a pure inertance Lt, so that Zt(w) = jwLt. Fig. 3 shows our simplified model with an inertive supraglottal loading of magnitude Lt. The flow Ug for this model is governed by the following differential equations:

With the added condition that Ug(0) = 0.
As can be verified by substitution in the equations, the solution for this set of differential equations is

For 1 £ t £ 2 the solution has 2 forms, depending on the magnitude of Lt:

These functions are plotted in Fig. 3 for some representative value of Lt. It can be seen that inertive loading would tend to give the flow pulse its often-noted skew to the right and rapid termination. Since the high frequency energy produced at a discontinuity of slope tends to be proportional to the change of slope at the discontinuity. the high frequency energy produced at the termination of the glottal pulse can be greatly increased by inertive loading. The terminal slope increases rapidly with Lt. even at values of Lt which do not drastically reduce the peak amplitude of the flow waveform. This differs from the dissipative case, in which a steep termination is obtained only by limiting the pulse height, i.e., in which the proportion of high frequency energy is increased by reducing the low frequency energy (which varies with the pulse height). In the inertive case, there is an actual increase in high frequency energy caused by the loading.

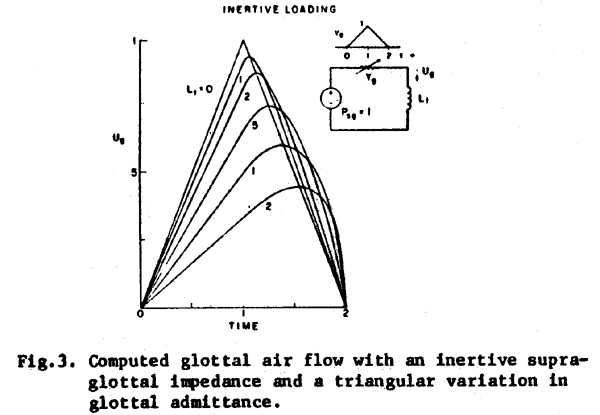
It can also be seen in Fig. 3 that the response between t = 0 and t = 1 is a linear increase in flow with a smaller slope than for the non-interactive case. Thus the high frequency energy produced at the onset of the glottal pulse is reduced. In the limit. with high values of Lt, Ug approaches a "sawtooth" or "ramp" waveform with a linear increases from zero flow at t = 0 to a peak flow of 2/(Lt + l) at t = 2. followed by a sudden decrease to zero flow at t = 2. The spectrum of such a pulse falls off at only 20 dB/decade compared to the 40 dB/decade fall-off for the triangular pulse that occurs with Lt = 0.

However, the increase of high frequency energy produced by the glottal closure is not just an asymptotic affect that is present only with high values of Lt. The increase of terminal slope occurs with relatively small values of Lt. and in fact. the terminal slope becomes infinite for values of Lt greater than unity. This result can be seen from the time derivative of Ug(t). For 1 £ t £ 2 the derivative is

For 0 £ t £ 1 the slope is l/(L+l) for all values of L. Thus the slope at the onset of air flow decreases gradually with Lt. while the terminal slope increases rapidly for values of Lt approaching unity as the term l/(Lt-l) increases and dominates the second term. For Lt > 1 the second term becomes infinite as t approaches 2, since (1/Lt - 1) is negative. Inertive loading also delays the peak of the volume velocity flow. For the simple model of Fig. 3, the time at which Ug is maximum can be calculated by setting the time derivative equal to zero and solving for t. This procedure yields:

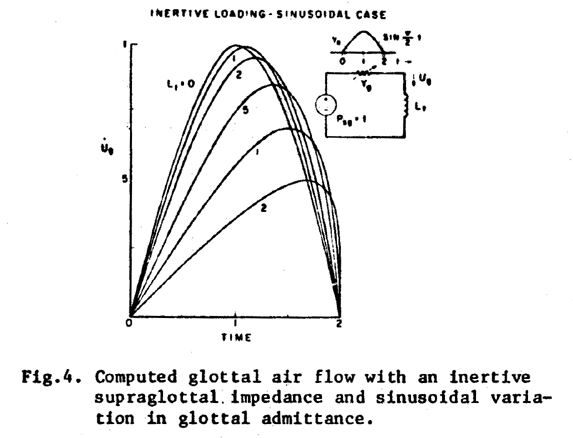
To show the effect of inertive loading with an admittance waveform that is more rounded near the peak than is a triangle, Fig. 4 gives the flow that would result if Yg were one-half cycle of a sinusoid. Since we have not derived a closed-form solution for this case, the curves were obtained by means of a digital simulation of the differential equation. With the sinusoidal admittance, the peaks of the flow waveforms become more rounded than for the triangle, especially for small values of Lt. In addition, the peak of the flow waveform is delayed somewhat more, as a function of Lt, than for the triangular admittance function, and the value of Lt at which the derivative at t - 2 becomes infinite appears to be somewhat less than unity. Otherwise, the responses for the sinusoidal and triangular cases are very similar. The insensitivity of the general form of the volume velocity to the details of the glottal admittance function with higher values of Lt supports our assumption that a rough approximation to the actual admittance can be informative.

Another simplification that we have made in modeling the glottal admittance waveform has been to assume that the admittance before and after the glottal pulse is zero. Inverse-filtering studies and motion pictures of the glottis during voicing have shown that there is often a patent air path between the arytenoid cartilages. This flow path would tend to show up in our model as a fixed impedance (or admittance) in parallel with the time-varying component. In the non-interactive model, the result would be primarily to offset the flow waveform from zero flow, without much change in the shape of the glottal pulse. However, with inertive loading assumed, the added admittance would alter the form of the differential equation and therefore affect the pulse waveshape, primarily near the onset and offset of the glottal pulse. 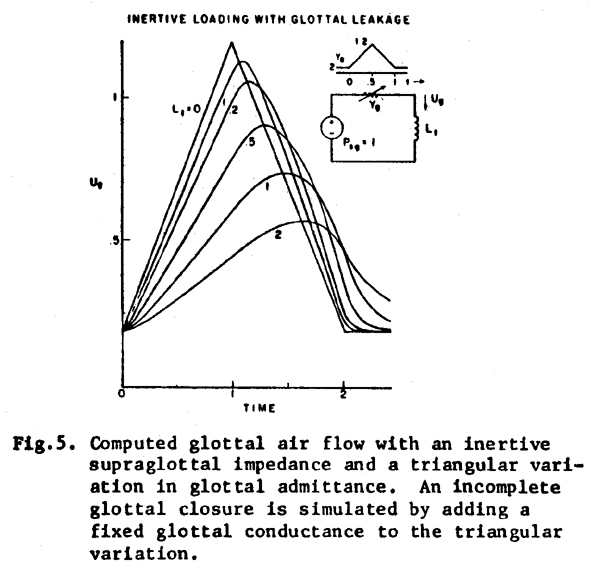To see in more detail that the effect of such glottal "leakage" might be, we have, in Fig. 5, inserted a fixed admittance, Yg - l, of 0.2 times the amplitude of the time-varying component of Yg, Yg-ac in parallel with the time varying component. In doing this, we have again assumed a linear model for the glottal admittance and neglected the inertive component. Offsets of this magnitude are commonly observed during inverse-filtering of oral air flow, and may be much larger in pathological voice, or, naturally, during breathy voice. The general result of this glottal leakage is to cause a gradual onset of the glottal flow pulse, and a more gradual offset, with less high frequency energy produced at both locations.

The reduction of high frequency energy at the instant of glottal closure is of special interest because of its strong potential affect on voice quality. Without "leakage," the high frequency energy is produced by the sealed glottis forcing the flow to zero, in opposition to the influence of the inertance, which acts to continue the flow. With leakage, the decrease in Yg stops when Ug is still decreasing slowly. At that instant the glottal flow pattern changes to a more gradual, exponential decay, with a time constant (Yg-l)(Lt). It may be significant that, according to this simple model, the stronger the source-tract interaction (the higher the value of Lt) the greater is the degradation of the high frequency energy caused by Yg-l. In other words, according to this model, inertive loading of the glottal source will cause an increase in high frequency energy on glottal closure only if there is very little air leakage during the interval of vocal fold closure.



Before turning to the experimental corroboration of acoustic loading-effects on the glottal waveform, we should note that the above theoretical development has been for a symmetrical glottal admittance pulse. Though a symmetrical pulse (whether triangular or sinusoidal) may be a good first approximation to admittance functions derived from projected area measurements, there may be a good deal of dissymmetry in individual cases. To see how such dissymmetry could interact with loading effects, we solved the differential equation resulting from the triangular admittance function pulse used for Fig. 3 (having a total width or duration of two, a peak value of unity and no "leakage"), but with the peak occurring at some arbitrary time Tm. instead of at t = 1. If Tm is between zero and one, the admittance function tilts to the left, and if Tm is between one and two, the tilt is to the right with Tm = 1 being the case illustrated above in Fig. 3. The differential equations for Ug would then be:

As long as Lt is not exactly equal to unity (since Lt = 1 results in an indeterminacy in the solution form) the solution to these equations is

where

As for the special case of Tm = 1 (a symmetrical pulse), the onset of the pulse is linear, and the offset is steeper than the onset. However, the skew of the admittance pulse is now a function of both Lt and Tm. We illustrate this by showing that the "critical" value of Lt, i.e., the value above which the derivative becomes infinite at t - 2, will vary with Tm. The relationship can be derived by first differentiating Ug in the interval Tm £ t £ 2:

As t approaches two, this function becomes infinite for values of Tm and Lt that make the exponent in the first term negative. This occurs for values of Lt greater than (2 - Tm). Thus, if the admittance pulse is skewed to the right (Tm > 1) the flow termination will become infinite at smaller values of Lt, and vice-versa. For example, if Tm = 4/3, for a rather high but possibly attainable opening time to closing time ratio of two, the critical value of Lt is reduced to 2/3 as compared to the value of unity that holds for the symmetrical admittance function.

THE MEASUREMENT OF SOURCE-TRACT ACOUSTIC INTERACTION

Though an inertive loading of the glottal source would produce flow waveforms very much like those observed by using standard inverse-filtering techniques given a symmetrical variation of glottal admittance it still remains to be shown that this type of glottal-supraglottal interaction is significant in such activities as speech or singing. There are a number of ways that we can study this during actual vocalizations. The most direct method might be to measure Zt somehow, but this requires the measurement of the pressure just above the glottis, and is difficult to implement. (However, see Dr. 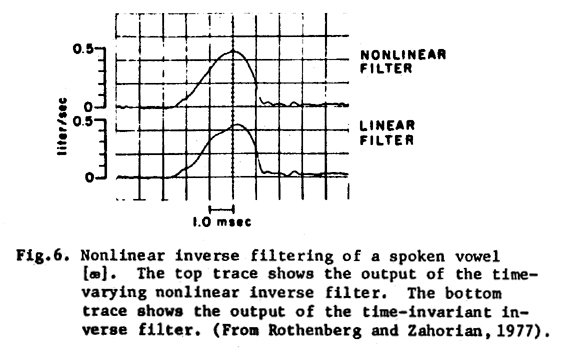Koike's Chapter 14 in this book.) Using another approach, we have attempted to implement. a "nonlinear inverse filter" in which some of the effects of the glottal-supraglottal interaction are removed (Rothenberg and Zahorian, 1977). The resulting waveform, shown in Fig. 6, is more directly related to Yg than is the actual flow Ug. To aid in visualizing the assymetry of each waveform, the connected lines above the waveform were drawn in to match the maximum slopes of the rising and falling segments, neglecting the oscillations at the frequency of the first formant in the case of the. linear filter. It can be seen that in this case the supraglottal impedance did cause an alteration of Ug similar to that produced by inertive loading in our model.

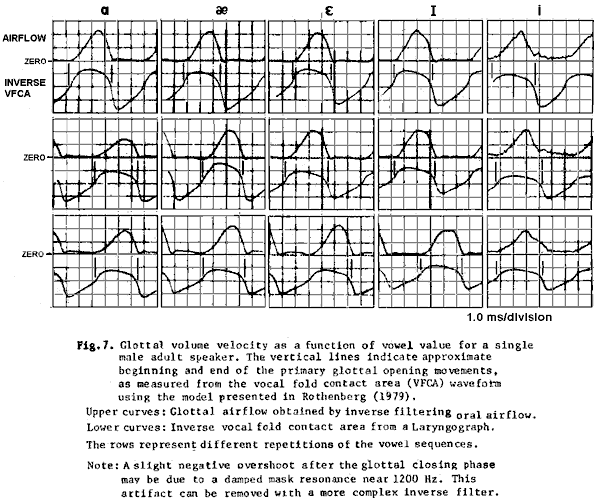
Another approach in measuring the affect of Zt is to change Zt while keeping the glottal area function approximately invariant. One way this can be done is by changing the vowel value. In the example in Fig. 7, the glottal flow was measured by inverse filtering oral air flow, while vocal fold movements were monitored by simultaneously recording the vocal fold contact area (VFCA) waveform obtained from a Laryngograph (Fourcin, 1974). The VFCA waveform is shown inverted in the figure, since the Inverse. VFCA waveform tends to rise and fall with the glottal airflow. The samples shown in the figure were from the center of the vowel in the nonsense syllable /b Vowel p/ in the syllable sequence /b a p b ae p ---/. Each row in the figure represents one such sequence, with the first two sequences (top two rows) spoken slowly enough so that each vowel had a distinct steady-state segment, while the last sequence (bottom row) was spoken at a natural rate. Vocal effort was at a moderate conversational level. The stop consonants help assure a good velopharyngeal closure during the vowel, which is important for accurate inverse filtering. Filter parameters corresponding to the frequency and damping of the first three formants were adjusted manually during a repetitive playback of the vowel sample, using the VFCA waveform as an aid in defining the glottal closed and open periods (Rothenberg, 1979). The low-frequency response limitation of the standard automatic amplitude control and high-pass filtering in the Laryngograph probably caused a slight falling of the inverse VFCA trace during the glottal open phase, but this distortion should be similar for all samples.

Except perhaps for the first (topmost) repetition of /a/ and the second (middle) repetition of / ae /, a constancy of the VFCA waveform between samples suggests that the differences in the Ug waveform were not caused by different vibratory patterns of the vocal folds. We refer here to the general shape of the waveform and not the amplitude, since the waveform amplitude depends on the larynx position relative to the electrodes, and therefore can vary with the vowel articulation.

If the two samples having a non-representative VFCA waveform are ignored, the figure shows that, of the vowels tested, those with a constriction closer to the glottis and a higher first formant (at the left in the figure) tended to have a glottal flow waveform which was more skewed to the right, with a steeper flow termination, and I therefore might be expected to have more high frequency energy generated by the termination of tile glottal closure. In fact, for the /i/ samples shown, the sharpest discontinuity in waveform slope, and therefore greatest production of high-frequency energy, appears to be at the peak of the waveform, and not at the instant of glottal closure. The overall shapes of the flow waveforms in Fig. 7 are roughly similar to those produced by the model in Figs. 3 and 4, as inertive loading is varied, except for the added oscillations at the first formant frequency. The oscillatory component of the interaction is not included in our simple model. Though there was considerable waveform variability between speakers, the general trend toward more dissymetry with vowels closer to /a/ was also found in the samples from two other speakers tested. one male and one female.

These results are at least roughly consistent with calculations made from a simple model of the vocal tract. For a lossless supraglottal vocal tract 17 cm long, with a uniform area of 5 cm², the impedance Zt will be inertive for frequencies below the first formant frequency of 500 Hz (or. more precisely, below a frequency just slightly under the first formant). The magnitude of this impedance will be approximately 8 tan(w/2000) in either acoustic ohms or units of cm H²O per liter/sec. In order to represent the actual vocal tract impedance below F1 by a pure inertance. it is necessary to find a linear approximation to the actual impedance function. Assuming that in our example the frequencies between 125 Hz and 375 Hz. representing an F0 of 125 Hz and the second and third harmonics are of most interest we can make a linear approximation by estimating Lt as the derivative of |Zt| with respect to w at some intermediate frequency, say 250 Hz:

To normalize Lt to the scales used for Figs. 2, 3, and 4, it is necessary to multiply by the actual maximum glottal admittance (or conductance, ignoring Lg) and divide by the actual time for one-half the glottal pulse (approximately 2 ms at F0 = 125 Hz). In calculating interactive effects, the differential conductance dUg/d(Psg - Pt) should be used. For a flow of 500 ml/sec and a maximum glottal area of 0.16 mm², typical adult male values, the maximum glottal conductance would be approximately .05 in cgs units, as computed from A²/rUg (Flanagan, 1958; Fant, 1960). Defining Lt as the value of Lt normalized to the scales used for Figs. 2, 3, and 4, we obtain:

Vowels with a higher F1 would be expected to yield a value of Lt that is valid over a wider frequency range, since more harmonics would be included before Fl is surpassed and the reactance becomes compliant. In addition, vocal tract configurations in which the pharynx is more constricted than for a neutral vowel might be expected to lead to a higher value of Lt. Since the value of Lt also depends upon the maximum glottal admittance, a vocal fold vibratory pattern that resulted in a wider than average glottal opening would also increase Lt, as would the inertive component of an unusually pronounced constriction at the entrance to the larynx or at the false vocal folds. Thus a value of Lt of at least 0.5 for a back vowel such as /a/ in some speakers is not inconceivable. Any glottal inertance would add to this figure.

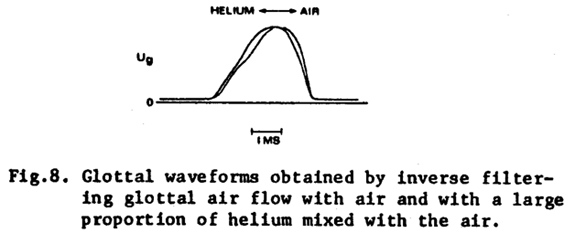
Finally, we have also tested for the presence of supra-glottal loading effects by comparing vocalizations made with air and with a large proportion of helium mixed with the air. By reducing the acoustic inertance in the vocal tract, the helium would be expected to reduce any supra-glottal loading effect, if present. (Though, unlike the change of vowel value, the use of inspired helium also affects the glottal inertance. To affect only the acoustic loading, it would be necessary to introduce the helium only into the supraglottal pathway.) Fig. 8 shows the general result we obtain. Both waveforms in the figure were obtained by inverse filtering the oral volume velocity for a male adult holding a vocal tract position for an /ae/ vowel. The fundamental frequency in each case was about 110 Hz. It can be seen that the symmetry of the waveform increases significantly with helium displacing some of the air.

CONCLUSIONS

It appears that the often-noted skewing of the glottal flow waveform which results in the primary vocal tract excitation being at the instant of glottal closure can be caused by a combination of factors, including dissymmetry in the glottal admittance function, air displaced by vocal fold motion, and acoustic interaction with the supraglottal impedance. The inertance of the glottal slit may also be a factor, at least at the smaller glottal openings, when this inertance is largest.

To study the effect of acoustic interaction, we have defined a normalized supraglottal inertance Lt, which approximates the actual loading of the glottis at frequencies between F0 and F1, assuming F1 is appreciably larger than F0. This model for the supraglottal loading indicates that for a symmetrical triangular admittance pulse the effect of acoustic interaction becomes large if Lt is close to or exceeds unity, since at Lt = 1 the derivative of the glottal flow becomes infinite at the instant of glottal closure. This critical value of Lt will vary with the symmetry and general shape of the admittance pulse, but appears to remain in a range of roughly 0.5 to 2.0 for the type of admittance variation to be found in normal speech. The model also indicates that at higher values of Lt the volume velocity waveform tends to have a characteristic shape which is rather insensitive to the details of the glottal admittance function.

A rough analysis of the magnitude of the supraglottal vocal tract impedance shows that values of Lt of at least 0.5 are not implausible, with the value in any given case being a function of the vowel value. the maximum admittance of the glottis during the glottal cycle and the configuration of the larynx above the vocal folds.

A simple representation of the glottal admittance function that would result from an incomplete vocal fold closure during the glottal cycle indicates that this factor is also important. in that it can appreciably modify the effect of source-tract acoustic interaction. However, small leakage paths may not be as significant as our results in Fig. 5 suggest, since we have neglected the glottal inertance, a factor that could be relatively large with a small opening.

Our results demonstrate that acoustic interaction can cause the glottal source waveform to vary widely as a function of vowel value and F0, since the first formant must be high compared to F0 in order for the supraglottal loading to be inertive at an appreciable number of glottal harmonics, and because the magnitude of the impedance below F1 varies as a function of vowel value. It is also possible that different pronunciations (allophonic variations) of the same vowel phoneme can result in appreciably different source spectra because of differences in the impedance seen by the glottis. The degree to which this phenomenon can explain differences in voice quality in speech and singing would be an interesting subject for future research.

ACKNOWLEDGMENTS

The work described here was supported by research grant NS08919 from the National Institutes of Health. James T. Mahshie assisted in the experimental work, and the author was fortunate to have the help of Wilbur R. LePage in the solution of the differential equations.

REFERENCES

Fant, G. (1960) acoustic theory of speech production. s-Gravenhage: Mouton.

Fant, G. (1979) Glottal source and excitation analysis.

Royal Inst. of Tech. (Stockholm): Speech Trans. Lab., Quart. Prog. and Stat. Rep. 1/1979, 85-105.

Flanagan, J.L. (1958) Some properties of the glottal sound source. Journ. Speech and Hearing Res. I, 99-116.

Flanagan, J.L. (1968) Source-system interaction in the vocal tract. Ann. N..Y. Acad. Sci..(Sound Production in Man), 155, 9-17.

Flanagan, J.L. and Ishizaka, K. (1978) Computer model to characterize the air volume displaced by the vibrating vocal cords. J. Acoust. Soc. Am. 63, 1559-1565.

Fourcin, A.J. (1974) Laryngographic examination of vocal fold vibration. In Ventilatory and phonatory control mechanisms, B. Wyke (ed.) Oxford: Oxford University Press, 315-333.

Holmes, J.N. (1962) An investigation of the volume velocity waveform at the larynx during speech by means of an inverse filter. In Proc. IV Int. Congr. Acoust, Copenhagen, Denmark, Aug. 1962.

Miller, R.L. (1959) Nature of the vocal cord wave. J. Acoust. Soc. Am. 31, 667-679.

Rothenberg, M. (1973) A new inverse-filtering technique for deriving the glottal airflow waveform during voicing. J. Acoust. Soc. Am. 53, 1632-1645.

Rothenberg, M. (1979) Some relations between glottal air flow and vocal fold contact area. In National Institutes of Health, Proceedings of the Conference on the Assessment of Vocal Pathology (to be published).

Rothenberg, M. and Zahorian, S. (1977) Nonlinear inverse filtering technique for estimating the glottal area waveform. J. Acoust. Soc. Am. 61. 1063-1071.

Home

Publications

E-mail

Papers online