Publications of Dr. Martin Rothenberg:

In the model for the production of voice that has dominated the literature on speech and singing until relatively recently, the glottis acts as a source of volume velocity that is independent of the time-varying supraglottal acoustic load imposed by the maneuvers of the various articulators. This view was a valuable one in the effort to identify the primary acoustic parameters that convey the linguistic and emotional message intended by the speaker or singer and has been extremely useful in such practical applications as synthesis and analysis of speech and singing.

However, much recent research has been focused on a reconsideration of the independent source-tract model. In such a reconsideration, the supraglottal system can be viewed as producing pressure variations above the glottis that may have two possible effects: (1) these pressures can affect the pattern of air flow within the glottis, with the motions of the vocal folds relatively unaffected, and (2) the resulting changes in glottal airflow and intraglottal pressure can alter the vibratory pattern of the vocal folds. The success of the independent source-tract model was based primarily on the high acoustic impedance of the glottal orifice compared to the impedance of the supraglottal vocal tract during the central or target segments of most vocalic speech sounds. Thus the supraglottal pressure in those cases was always small compared to the subglottal pressure. (We ignore in this paper the periodic variations in subglottal pressure that occur during voicing. Although the subglottal acoustic system is, of course, also of interest in some situations, it is not under active control and does not vary much during the act of speech or singing.)

However, the independent source-tract model was also successful because of the relatively high impedance of the vibrating vocal cords or, more precisely, of the mechanical-aerodynamic system that is responsible for the generation of the periodic variations in glottal dimensions that are responsible for voice production, compared to the typical supraglottal acoustic impedance. Thus, even when a supraglottal articulatory constriction tended to cause enough oscillatory back pressure to affect the pattern of glottal air flow, the vibratory pattern of the vocal folds tended to remain the same, apparently until the constriction was enough to raise the average supraglottal pressure to an appreciable fraction of the subglottal pressure. The hedge "apparently" in the previous sentence is necessary, since this latter hypothesis has been documented only sparsely. This lack of empirical verification is probably due to the difficulty of recording laryngeal function during transient constrictions and the difficulty of ensuring that any change (or constancy) in the laryngeal vibratory pattern was not caused by a simultaneous change in laryngeal muscle tension. Thus, any correlation noted between either F0 or average airflow (the vibratory parameters most easily monitored) and the degree of constriction in a vowel or consonant could have a multitude of causes.

Early attempts to bypass these measurement difficulties by a simulation of the entire laryngeal-acoustic system have been problematic because of the crudity of the models used compared to the complexity of the actual system. Recent more detailed models show more promise in this regard, tending to support the assumption of a high impedance mechanical-aerodynamic vibratory mechanism (Titze, 1983), and have resulted in some significant generalizations about the effect of average transglottal pressure on the vibratory pattern (Titze, 1986). However, extrapolations from such complex models will remain tenuous without some means of empirical corroboration.

As a consequence of these difficulties, in considering the effect of articulatory changes on the vocal fold vibratory pattern, we are basically left with the model of a glottal area function that, for a given average subglottal pressure, depends only on the amount of tension in the laryngeal musculature, except in the neighborhood of a complete (or almost complete) articulatory constriction. According to this model, as such a constriction is approached, the vocal fold oscillations will decay in a manner dependent on the degree to which the supraglottal air volume can absorb the glottal airflow without the average supraglottal pressure rising (Rothenberg, 1968). After such a constriction is relaxed, the oscillations are assumed to quickly return to the pattern determined by the laryngeal musculature and average subglottal pressure. However, this model is likely to be inadequate for describing the use of the voice under the strenuous demands that may be placed on it in applications, such as singing, and may even be inadequate for some applications in describing the use of the voice in normal speech.

We focus here on one of the more demanding uses of the voice in singing, namely, the upper range of the voice of the trained soprano. It is well documented that opera-style soprano singers tend to tune the first formant to the voice pitch in this range (Sundberg, 1975), and we have shown that in a very efficient soprano voice the acoustic interaction between this resonance and the voice source can act to reduce the airflow significantly while increasing the richness of the tone by strengthening the higher harmonics (Rothenberg, 1986). However, the question left unanswered is if the tuning of F1 and the very strong resulting oscillatory pharyngeal pressure variations at F1 (Schutte and Miller, 1986) are also influencing the nature of the oscillations of the vocal folds, even when the average supraglottal pressure is small compared to the subglottal pressure.

METHOD

In the experiments reported here, the effective length of the vocal tract was momentarily extended, and the formants thereby lowered, by coupling a length of hard-walled plastic tubing to the mouth opening. The tubing had an internal diameter similar to that of the widely open mouth and was momentarily coupled to the lips by one of the two schemes shown in Figure 1. Although the full length of the tubing was about 30 cm, the acoustically effective length, i.e., the distance from the end near the mouth to the first set of holes, was only about 10 cm. The second set of holes may have been redundant, but they ensured that there was no buildup of average oral pressure while the tube was coupled to the mouth, either due to the airflow of the breath or due to the air displaced by the movement of the tube. This was verified by measuring oral pressure in one subject. The tube parameters were chosen so as to cause a perturbation extreme enough to ensure some movement of F1, regardless of the vowel articulation. Since measuring the resulting formant changes during the actual singing task would be difficult because of the high pitches tested, the likelihood of a reduction in F1 was verified by measuring on a spectrogram the formant change during a similar vowel produced at a much lower pitch. The reduction in F1 was about 220 Hz.

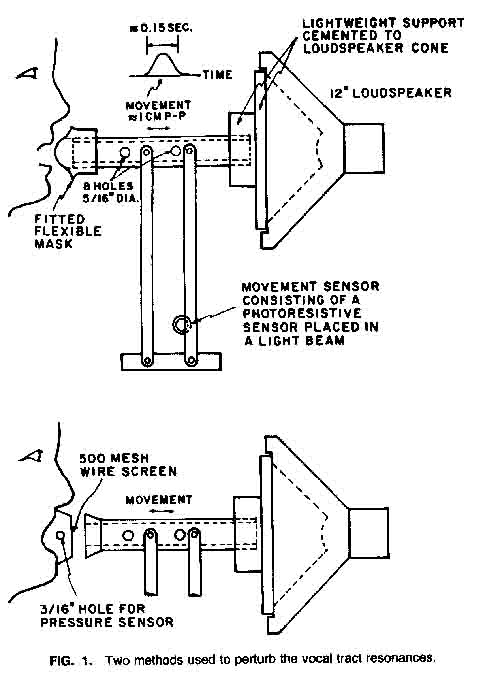
In the arrangement at the top of Figure 1, the mask at the end of the tube was normally about 1 cm from the face and moved into contact with the face near the extreme point in its travel. This initial spacing was close enough so that the displacement of the tube from its initial position could be equated roughly with the degree of detuning. The motion of the tube was monitored by the photoelectric sensor near the bottom of the apparatus. The motion was induced by a low-pass filtered electrical pulse applied periodically to an electromagnetic driver (a modified loudspeaker) at 0.75 pulses/sec. The duration of the movement pulse, about 0.15 sec, and the smooth shape of the pulse were chosen to generate a minimal acoustic disturbance.

The pulse was also short enough so that there could be no appreciable compensation by the subject for the acoustic effect of the tube. In initial pilot tests, one subject apparently attempted to make some form of compensation, but this resulted primarily in a change in voice quality after the pulse was gone (the tube removed from the mouth). An instruction to the subject to ignore the perturbation caused by the pulse rectified this problem, and our records showed no recurrence.

Though the dimensions of the acoustic (mouth-mask-tube) system and the results reported assured us that the first formant was in fact being lowered significantly by the added tube, no attempt was made to track the movement of the formant as a function of the tube position. Then in the second arrangement, shown at the bottom in Figure 1, a small mask was tightly
coupled to the face around the mouth. During the pulse, the tube was moved to approach the outlet of this mask. This arrangement allowed us to measure the airflow from the mouth by making the mask into a wire screen pneumotachograph (Rothenberg, 1977), and also made a more reproducible variation in acoustic coupling as the tube moved. The disadvantage was that the singer had to adapt her (uncoupled) voice production to the presence of the small mask and wire screen. The singers reported no special difficulty in doing this, but the naturalness of the resulting uncoupled voice must still be suspect.

The reaction of the vocal fold oscillations to the acoustic perturbation was monitored primarily by an electroglottograph (EGG). The version used was made in our laboratory and had the concentric electrode configuration used in the Laryngograph or Kay Elemetrics models. The signal was linear-phase high pass filtered at 50 Hz to remove low frequency noise without distorting the waveform within a glottal cycle. The EGG gives little direct evidence about the motion of the vocal folds when they are not in contact; however, if there is an appreciable period of vocal fold contact in a particular voice, as was the case for the voices of both subjects used, the EGG signal could at least identify with some degree of certainty when the acoustic perturbation had no effect on the vocal fold motion, since this would be reflected in an unchanging EGG signal.

A Racal FM tape recorder, at 30 inches/sec, was used to record the EGG signal, a signal from a microphone a few inches from the mouth, the tube motion waveform, the voice fundamental frequency as extracted on a period by period basis from the EGG signal, and, with the second arrangement in Figure 1, both the wideband airflow and a low passed (at 100 Hz) version of the airflow. Airflow was calibrated with a Gilmont rotameter. The signals were replayed, in various combinations, as required, into a four-channel hot-wire chart recorder, with a 32: I speed reduction in the tape recorder providing an effective frequency response to about 1,600 Hz.

The subjects were two sopranos with considerable professional experience who were former students in the voice department at the Syracuse University School of Music. They were instructed to sing a number of scale passages at the high end of their range, with each note being held long enough to include two acoustic perturbations.

RESULTS

We found that for each subject there was a range of pitches for which the EGG waveform was significantly perturbed and other pitches for which the effect on the EGG waveform was consistently small. The results were similar for both arrangements in Figure 1, although the effect appeared to be stronger with the first arrangement (without the wire screen), as might be expected.

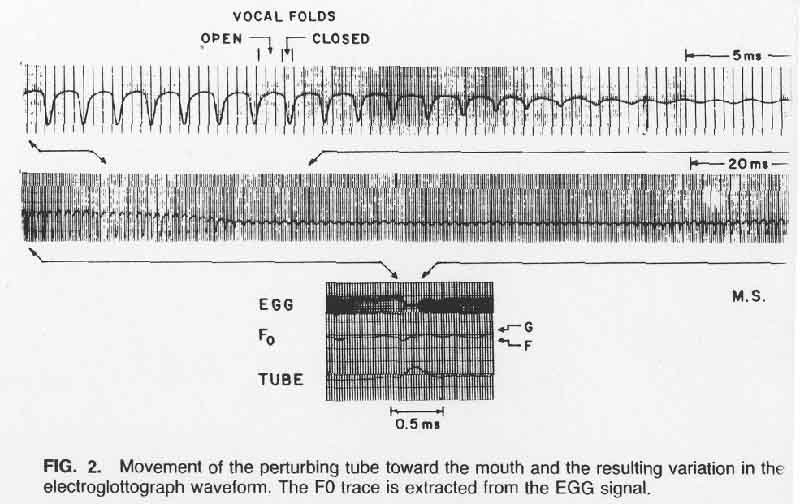
A result that was typical of the stronger perturbations for both subjects is shown in Figure 2. The polarity of the EGG waveforms was chosen such that increased vocal fold contact is in the negative direction. It can be seen that the primary effect on the EGG waveform is a reduction in amplitude and width of the negative-going pulses that occur when the vocal folds come into contact. These effects were roughly proportional to the displacement of the tube, both as the tube approached the mouth and as it receded from it.

The frequency of the EGG pulses in Figure 2, i.e., the pitch being sung, varied very little in this case. The small transient changes in the F0 trace as the tube approached and receded from the mouth, less than a semitone at maximum, could have been caused primarily by the change in EGG waveform and not by the frequency of the underlying vocal fold vibrations. F0 was computed as the inverse of glottal period, with the glottal period estimated from the negative-going zero crossings of the high-passed EGG signal (with less contact positive, as in Figure 3). As the waveform changed, this zero-crossing instant occurs at a different place in the vibratory cycle, to yield an apparent change of the glottal period during the time the waveform is changing. Rough calculations show that these perturbations in measured F0 would agree in polarity with those shown in the F0 traces and would also agree in order-of-magnitude.

The two possible interpretations of the change in the negative-going pulses in the EGG waveform are shown diagramatically in Figure 3. The underlying assumptions in the figure and examples from speech can be found in Rothenberg and Mahshie (1988). Figure 3 basically illustrates that the changes noted in the EGG waveform could conceivably be caused by either a variation in the degree of vocal fold abduction or a variation in the oscillatory energy, or some combination of these two effects. Although the two effects are difficult to distinguish from the EGG waveform alone, they would each have a different effect on the glottal airflow. Vocal fold abduction would tend to increase the average value of the airflow waveform, whereas a reduction in oscillatory energy would tend to have little effect on the average flow, perhaps reducing it slightly. Examination of the average airflow traces for both subjects showed no increase in airflow correlated with the change (reduction in amplitude) in the EGG waveform. Since we can also find no physical reason why the change in vocal tract tuning would primarily affect the vocal fold abduction, we conclude that the primary effect of the detuning was a change in the oscillatory energy of the vocal folds.

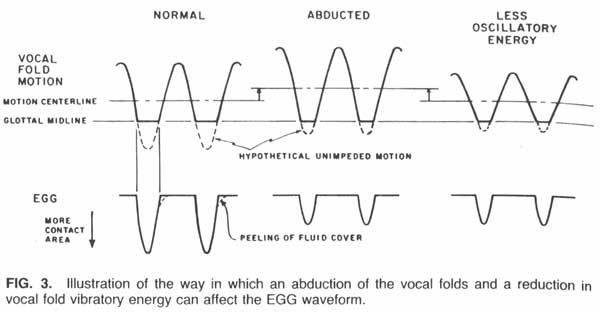
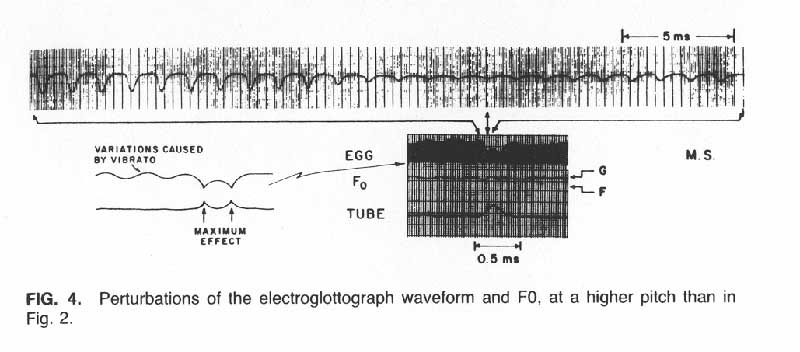
When the EGG signal was affected by the vocal tract detuning, the pattern noted was usually similar to that in Figure 2, i.e., the waveform decreased in amplitude during the detuning in a manner somewhat proportional to the degree of detuning (the closeness of the tube to the mouth). According to the model of Figure 3, this pattern would be interpreted as indicating that the amplitude of the vocal fold oscillations decreased roughly in proportion to the degree the first formant was lowered. However, in some cases with one subject, the pattern shown in Figure 4 was observed. The amplitude of the negative-going pulses reached a minimum when the tube was about halfway to the mouth and recovered most of its lost amplitude when the tube approached more closely. The interpretation we make of this pattern is that there was a critical value of F1, slightly lower than its unperturbed value, at which the vocal fold oscillatory energy was maximally depressed. In future research, this assumption can be tested by varying the degree to which the tube approaches the mouth, with the same subject and pitch, and comparing the resulting EGG traces. (See reply to Dr. Ishizaka in the discussion following this article.)

The model in Figure 3, assuming a sinusoidal vibratory motion, theoretically would allow one to estimate the degree to which the oscillations decreased from the change in the duty cycle of the EGG waveform until the point at which no vocal fold contact occurs, assuming, of course, that there was no simultaneous change in the degree of abduction (Rothenberg and Mahshie, 1988). Since the largest perturbations in EGG amplitude did result in no vocal fold contact, no precise estimate could be made of the degree to which the vocal fold oscillations could be reduced by the detuning. However, our rough estimate, using some extrapolation from the regions during which the vocal folds did make contact, was that in the stronger perturbations the oscillatory amplitude was reduced by a factor of about one half. In no case did the vocal fold oscillations cease entirely during a perturbation, as evidenced by a continuous acoustic waveform and also by the continuity of the small, almost sinusoidal component at F0 in the EGG waveform. In no case did a significant increase in EGG signal occur with detuning.

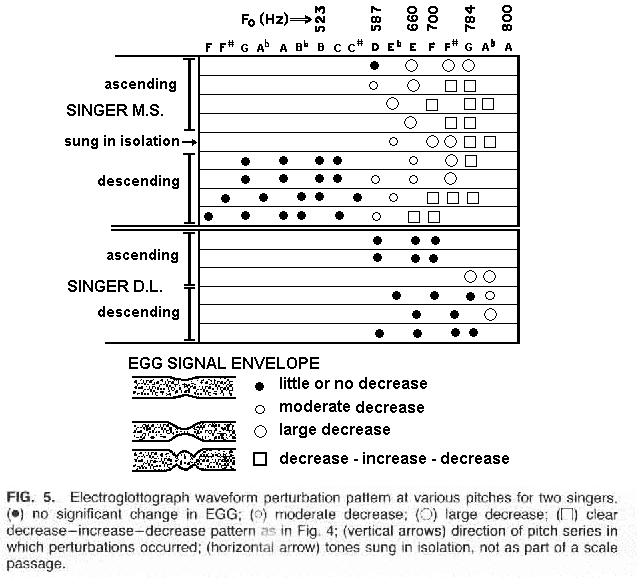
The pitches at which a perturbation in vocal fold amplitude were noted are shown in Figure 5. Each vocal tract detuning is indicated by a mark. A small dot indicates no significant change in EGG; a small circle, a moderate decrease; a larger circle a large decrease; and a square, a clear decrease-increase-decrease pattern such as in Figure 4. The arrows at the left indicate the direction of the pitch series in which the perturbations occurred, although it appeared that the direction had no effect on the results. The horizontal arrow indicates tones sung in isolation and not as part of a scale passage.

The subjects both showed EGG perturbations only at the higher pitches; however, the pattern of occurrence differed slightly. Subject DL only showed a perturbation at the highest notes, whereas MS showed perturbations throughout the pitch range in which the first formant could have been tuned to F0 for the vowel being sung ([a]). The interpretations we make of this patterning is that MS's productions are somehow less stable in their vocal fold oscillatory behavior than those of DL, although both would have to carefully control the vocal tract tuning at the top of their range.

Thus one might predict that DL would be able to maintain a stronger voice if the vowel was not chosen so as to match F1 to F0.

It is interesting that we did not measure any significant tendency for F0 to follow F1 during the detuning maneuver for these subjects (as might occur in the somewhat analogous case of a wind instrument). An auditory impression of a slight flatting of the pitch was apparently due to the reduction in amplitude of the tone heard.

CONCLUSIONS

It seems clear from this pilot experiment that the perturbation method described can be used to test for the sensitivity of a voice to a change in vocal tract resonance, at least for open vowels. It is also clear that singers may be expected to vary in the degree to which they employ tuning to create pressure-flow phase relationships at the glottis that maximize the oscillatory energy in the vocal folds, and it is likely that the degree of variation to be found among singers may be expected to be greater than that found between our two randomly chosen subjects.

On the other hand, we noted that for both singers the tuning had a uniformly negligible effect for pitches under D5 (about 600 Hz), much as is the case for normal speech-mode vocalization. Whether there may be other ranges of tuning sensitivity for sopranos or, for that matter, for other singers, is still an open question. However, one would search for such ranges near register breaks or other areas in which a physical oscillatory mechanism is being stretched to its limit.

The primary problem in the experimental technique used was the lack of a more direct observation of the amplitude of the vocal fold oscillations and the degree of abduction. Although a number of invasive visual methods come easily to mind, a noninvasive technique such as ultrasonic echoing from one vocal fold would be highly advantageous if an adequate resolution could be attained. Although the airflow measurements we made were of some help in checking for abductory movements, in general the airflow can be confounded by nonlinear acoustic interactive effects and is not always a good representation of glottal area.

ACKNOWLEDGMENTS

This research would never have been performed without the cooperation of Dolores Leffingwell, who as a student of singing and voice science in our laboratory repeatedly insisted that certain problems she had with specific notes in certain consonantal environments were worthy of a detailed consideration. Now studying at the Peabody Conservatory, she arranged a visit to Syracuse to be one of the subjects in this experiment. We also appreciate the kind patience of our second subject, Martha Sutter.

Donald Miller, our laboratory's resident professional singer and singing teacher, participated in the taking of data and in data analysis. Thanks are due also to Lowell Lingo, Ir., for building the apparatus used and the five previous versions required in its development.

REFERENCES

Rothenberg, M. (1968). The breath-stream dynamics of simple-released-plosive production. Bibl. Phonetica 6.

Rothenberg, M. (1977). Measurement of airflow in speech. J. Speech Hear. Res. 20:155-176.

Rothenberg, M. (1986). Cosi' fan tutte and what it means-or-Nonlinear source-tract acoustic interaction in the soprano voice and some implications for the definition of vocal efficiency. In: Vocal Fold Physiology: Laryngeal Function in Phonation and Respiration, edited by T. Baer, C. Sasaki, and K. S. Harris, pp. 254-263. College Hill Press, San Diego.

Rothenberg, M., and Mahshie, J. J. (1988). Monitoring vocal fold abduction through vocal fold contact area. J. Speech Hear. Res. (in press).

Schutte, H. K., and Miller, D. G. (1986). The effect of F0/F1 coincidence in soprano high notes on pressure at the glottis. J. Phonetics, 14 (3/4):385-392.

Sundberg, J. (1975). Formant technique in a professional soprano singer. Acoustica 32:89-96.

Titze, I. R. (1983). Approaches to computational modeling of laryngeal function: Successes and prevailing difficulties. Abstracts of the Tenth International Congress of Phonetic Sciences, Utrecht, The Netherlands, Foris Pub.

Titze, I. R. (1986). Mean intraglottal pressure in vocal fold oscillation. J. Phonetics 14(3/4):359-364.

DISCUSSION FOLLOWING ROTHENBERG PRESENTATION

Dr. Larson: Did the movement of the tube alter the length of the vocal tract?

Dr. Rothenberg: As the tube got closer to the mouth, there was still a gap between it and the vocal tract, but at the apex of its movement it actually did touch the mouth and then it was directly extending the vocal tract. Spectrograms made at lower values of F0 indicate that as the tube approached the mouth, the first formant gradually shifted until the tube actually touched, at which point there was a maximum lowering of the formant.

Dr. Stevens: I might suggest another possible explanation for the differences between the two subjects reported in your paper. For the vowel /a/, the first two formants can be assigned very roughly as resonances of the pharyngeal region and of the oral cavity. Which cavity goes with which formant might depend on the dimensions of the speaker or on the particular way the speaker makes the sound. It is possible that making a change in the resonance characteristics at the front of the mouth may not change appreciably the resonance of the pharyngeal cavity, which may be formant 1 for some speakers.

Dr. Rothenberg: We experimented in many ways with changing the tuning of the vocal tract. There are many experiments that one would like to do that are impractical, such as actually moving the tongue. We couldn't think of a practical way to perturb the acoustics in the back of the vocal tract and so we did the best thing we could do that would have some significant effect on Fl, even if F2 moved more than Fl. We may not have been changing the resonances in the best way, but it was the only practical way that we could think of. We did try a number of other methods, such as moving solid objects into the mouth or expanding a balloon in the mouth, but our final method seemed to be a reproducible, reliable way of producing a reasonably large effect.

Dr. Stevens: I just thought that, while the person was phonating, you could squirt a little helium into the mouth.

Dr. Rothenberg: Yes, we also tried that, but the helium couldn't be introduced and removed fast enough to eliminate the possibility of a compensatory change in articulation. That problem may still be worked out, but we haven't been successful.

Dr. Ishizaka: I was also once interested in the acoustic loading effect of the vocal tract upon vocal fold vibration. I conducted an experiment to measure the change in F0 due to the vocal tract load. A bazooka-like tube was used and the length of the tube was periodically changed. The subject put the tube in his mouth and was asked to utter a vowel in the presence of the change in the tube length. I found that F0 was changed when F1 of the combined vocal tract and tube coincided with F0. This result is in good agreement with the theoretical considerations of the acoustic loading.

Dr. Rothenberg: I recall a paper by Ingo Titze that relates to your comment. It describes how the vocal fold vibratory pattern may be susceptible to supraglottal air pressure variations in certain pitch ranges. We did expect to also find pitch variations as F1 was moved toward and away from F0; however, in these particular cases, we didn't find very much. It could be that if, as Kenneth Stevens suggested, we perturbed the acoustic characteristics of the vocal tract closer to the larynx, we might get a greater pitch variation. But it is easier to alter the formants by extending the vocal tract.

Dr. Titze: Just one brief comment. I think the paper you are referring to was for the SMAC 83 Conference in Stockholm. I tried to make some calculations as to what kind of relationship should exist between F0 and subglottal and supraglottal formants (first formants) in order to maximally reinforce the mean driving pressures on the vocal folds. It turned out that F0 should be approximately one half of the first subglottal formant frequency, around 300 Hertz. (Recall Ishizaka's measurement of the first subglottal resonance was around 600 Hz.) F0 could also be near the first supraglottal formant frequency for optimal driving conditions, but slightly below F1. For either of these conditions, when F0 was raised above the indicated optimal frequency, the phase relationship between the vocal tract pressure (sub- or supraglottal) and the aerodynamic driving pressure changed so that the acoustic pressure would no longer reinforce the aerodynamic driving pressure.

Dr. Isshiki: I wonder if, with a hard-walled tube, the effect of vocal tract loading on the vocal cord vibration may be exaggerated in relation to the more physiological condition. Did you intentionally exaggerate the effect in order to know the extreme case?

Dr. Rothenberg: Yes, we did, although I don't think that the formant damping differed much from the case in which F1 was shifted by a small change in the singer's articulation. On the other hand, shifting F1 greatly to match a much lower F0 by means of a hard-walled tube might be significantly different from the physiological case.